Clock / Project help

[unknown1]

Hello everyone,

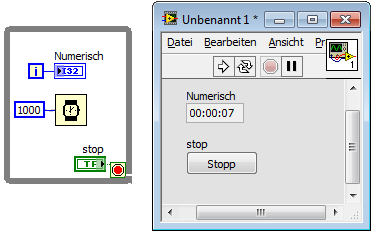
Is there a way to create a LINEAR number that increases as long as the loop is runnning? Simular to "LOOP ITTENERATIONS" in while loop. Im trying to create a simple clock type VI that will use that number.

Im basicly trying to make a CLOCK with simple math functions and a loop, but it keeps failing. The math looks good but the loop simply resets instead of adding an additional number to my X. What am i doing wrong?

Ive figured out how to make the output into minutes or seconds, and I think I can get a stucture to work with true or false number being LARGER THAN 60 and then minusing 60 from the X to reset the seconds.

Some one please help, ive been at this for like over 5 hours...

[Bob_Schor]

Have you ever heard of "Clock Arithmetic" (or Clock Mathematics)?  If not, type this phrase into Google and think about what you read.  Then think how to apply this (check out the Numeric functions).

Bob Schor

[crossrulz · Accepted solution]

You just need to use Quotient & Remainder to gets your minutes and seconds.

[GerdW]

Hi,

and I think all you need is this:

You can set the formatting of numeric indicators to a lot of different formats…

[unknown1]

Thank you, this works good

The seconds is the remainder, and I use the quotient for the calculaton of the minutes, and its quotient for hours. Works wonderfuly.

My math level is quite low, so i dont understand time calulations beyond the simple math, im not even sure how quotient and remainder works, its magic.

Thanks a bunch

[Yamaeda]

---

@unknown1 wrote:

Thank you, this works good

The seconds is the remainder, and I use the quotient for the calculaton of the minutes, and its quotient for hours. Works wonderfuly.

My math level is quite low, so i dont understand time calulations beyond the simple math, im not even sure how quotient and remainder works, its magic.

Thanks a bunch

---

Basically it's a divide, where you'll get the integer part (a normal divide rounded down) and the remainder (opt. it can be calculated as the fractional part times the divisor).

E.g. 4%3 = 1.33 rounded down = 1, 3*1 is however 3, so the remainder is 1. Q=1, R=1

It can also be described as "You can remove 3 from 4 1 time(s), and that'll leave you with 1 rest/remainder/unused"

11%4 "You can remove 4 from 11 2 time(s), and that'll leave you with 3 rest"

11%4 = 2,75 = Q 2, R (11-2*4 alt. 0,75*4) 3 = Q 2, R 3

/Y