IIR Filtering and response .vi: Butterworth filter magnitude response depends on sampling rate -why?

[windychris]

Hi folks,

I am not expert in filter design, only someone applying them, so please can someone help me with an explanation?

I need to filter very low-frequent signals using a buttherwoth filter 2. or 3. order as bandpass 0.1 to 10 Hz .

Very relevant amplitudes are BELOW 1 Hz, often below 0.5 Hz but there will be as well relevant amplitudes above 5 Hz to be observed.

This is fixed and prescribed for the application.

However, the sampling rate of the measurement system is not prescribed. It may be between say between 30 and 2000 Hz. This will depend on whether the same data set is used for analysing higher frequencies up to 1000 Hz of the same measurement or this is not done by the user and he chooses a lower sampling rate to reduce the file sizes, especially when measuring for longer periods of several weeks.

To compare the 2nd and 3rd order's magnitude response of the filter I used the example IIR Filtering and response .vi:

I was very astonished when I the found that the magnitude response is significantly influenced by the SAMPLING RATE I tell the signal generator in this example vi.

Can you please tell me why - and especially why the 3rd order filter will be worse for the low frequency parts below 1 Hz of the signal. I was told by people experienced with filters that the 3rd oder will distort less the amplitudes which is not at all true for my relevant frequencies below 1 Hz.  

In the attached png you see 4 screenshots for 2 or 3 order and sampling rate 300 or 1000 Hz to show you the varying magnitude responses without opening labview.

THANK YOU for your ANSWERS!!!

chris

[johnsold]

chris,

It would be much easier to give you a good answer it you posted your VI and actual data.

From the images I suspect that pert of the problem is that you have very few data points.  You will note that in several places the graph is in straight line segments. The segment from 0.2 to 0.6 Hz on the upper left image is an obvious example.  The response of the filter does not vary along straight lines like that.  Change the plot style to one which shows the data points to verify.

Lynn

[windychris]

Hello Lynn,

thanks for the answer. You are right that there are few points "behind" the curve in the graph, see png.

However, this is the filter response which Labview (2009) provides to me directly out of the "IIR Filter for 1 Channel. vi" in the "filter information" output cluster. Where up to now I do not know how to influence it - apart from adjusting the input parameters "IIR filter specifications". OK, I assume I have to gain more knowledge of this. The curve of the magnitude resonse dies not change when I change the number of samples of the input signal of the signal generator, only wehn I change the sampling rate.

I used directly the example vi from Labview with the name indicated in my first post "IIR Filtering and Response.vi".

So I assumed that everybody has it in his/her examples shipped with LV and it is not necessary to post it.

I just adjusted the size of the diagram of magnitude response to see the curves better as you see in the attached vi.

So I did no changes to the vital parts of signal generation and filter of the example. The screenshots are like they come from the example when using the option "one waveform" where I as user assume that this which is behind is quality-controlled by NI.

I was also astonished that the filter magnitude response is different to the one I copied out of graphs 1 year ago - but I unfortunately cannot reconstruct which example I used there...

Thanks for any further comments

chris

[johnsold]

chris,

There are so many examples that I do not know what is there and I missed that you were using one of the built in examples which ship with LV. The example has changed slightly in newer versions of LV also.

I see what you are asking about.

It appears that the Filter Information output is dependent on the sampling frequency. Lower sampling frequencies seem to give better resolution at the low frequency end. The relationship is not documented in the help for the VIs which generate that information. I was not able to find a combination which gave a nice display of the low frequency end of the filter response.

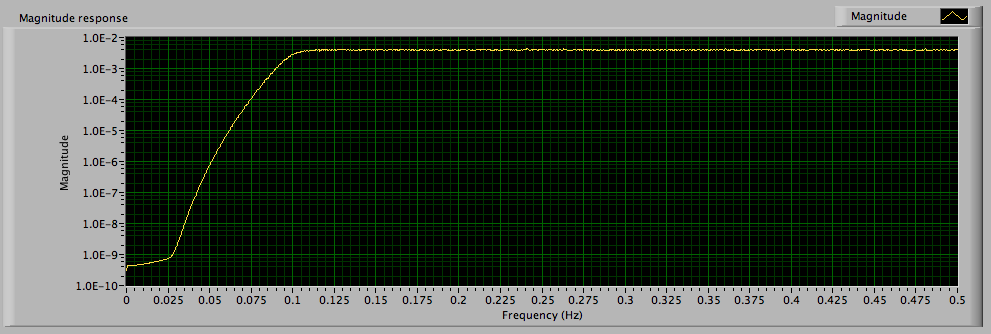
I tried an alternate approach: I generated a random noise signal. Uniform White Noise has a flat spectrum. Then I fed that signal to the filter and took the spectrum of the filter output.  The average of a large number of runs represents the spectral response of the filter.  This image was taken with Butterworth Bandpass, 12th order, Lower Fc = 100m, Upper Fc = 3.0, Fs = 20, #s = 50k.

Lynn

[windychris]

Good morning Lynn,

thank you for the quick response and the filter proposal.

The filter with 12th order which looks nicely in the range around 0.1 Hz. and seems to be suitable.

Unfortunately, if an ISO requires a Butterworth 2nd or 3rd order I cannot use a different order even if the filtered results appear to be useless in my eyes. But I will then use your approach I uderstood as the taking the difference of the spectra of filtered and unfiltered signal to compare the result for the measurement data. And then it seems to be necessary to develop recommendations for a standardisation of the measurement procedure that the results stay comparable.

Have a nice week, chris

[johnsold]

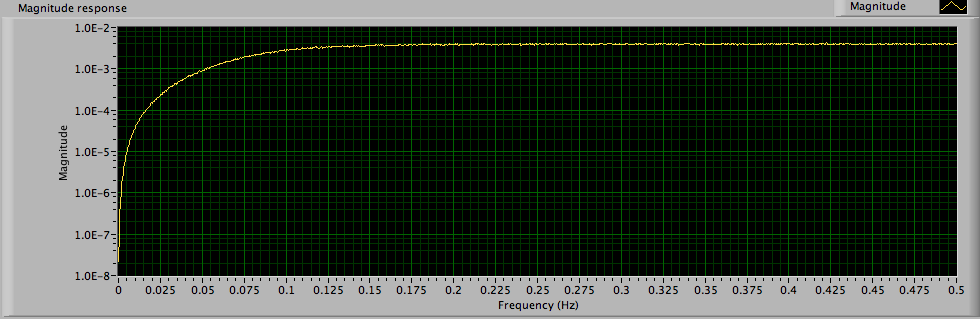
I do not recall why I used the 12th order filter.  Here is what I see with a second order filter.

Lynn

[windychris]

Good morning Lynn,

I do not understand your y axis. In my tests there is always a drop by 30% from 1.0 to 0.7 at the low frequency of 0.1 Hz as well as at the high frequency of 10 Hz which I cannot see in your graph - but you can see it in my graph and which corresponds to the - 3 dB drop i see when I turn on dB for the FRF parameters.

I attach what I did up to now by inserting the white noise generator and the frequency response function and also a "manual" averaging several responses. since the planned measuring time is at least 10 min I automated the calculation of the corresponding number of samples.

At least with the modifications I am relieved that the strange response from the example.vi does not appear any more and 2nd and 3rd order show the same -30% drop and the magnitude response shape is more what I expected before using the example..

however, despite the relatively large sample number, I find that the response for a single set is quite scattering.

Regards Chris

[camerond]

---

@windychris wrote:

Good morning Lynn,

I do not understand your y axis. In my tests there is always a drop by 30% from 1.0 to 0.7 at the low frequency of 0.1 Hz as well as at the high frequency of 10 Hz which I cannot see in your graph - but you can see it in my graph and which corresponds to the - 3 dB drop i see when I turn on dB for the FRF parameters.

---

Lynn's graph has a logarithmic Y scale, yours has a logarithmic X scale. That, and different scaling for the axes, accounts for the difference in the pictures.

Cameron

[windychris · Accepted solution]

Hello Cameron and thanks for clearing my lenses.

I now can proudly present the solution of my problem.

It seems to be purely a problem of the visualistion of the filter information through the magnitude cluster.

After looking into the IIR front panel I suddenly remarked that the "df" of the magnitude cluster is changing with the Fs of the input signal.

For a Fs of 30 Hz  the "df" is 0.03 Hz then you see that the filter curve with more points, see png.

For a Fs of 300 Hz the "df" is 0.3 Hz, hence the curve is more coarse with only 3 points between 0 and 1 Hz.

For a Fs of 1 kHz the df is 0.976 Hz so there are no points in the graph between 0 and 1 Hz.

This is strange that for constant Fs, the df of this cluster is NOT getting smaller with increasing the number of samples as it does in a FFT.

However I now trust the used filter since now the curves obtained with the way Lynn proposed and of the magnitude response from the filter information fit together.

Thanks for your support.

Merry Christmas and a happy new year to all.

Chris

[camerond]

Good. Now give Lynn a "thank you" with a Kudo and mark the message with your solution.

Cameron