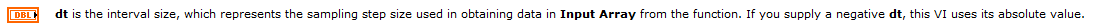- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathematical integration problem
Solved!07-12-2016 05:05 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello everyone,
Here is one VI I am working on... it is a Powermeter instrument which measures power via photodiode sensor. The instrument itself is set to measure power at 1 wavelength. I made the VI to sample a whole wavelengths range, with a certain step, and than integrate all the values of the measured power into one. This way I can include the visible wavelengts component into the final value of the measured power.
However, when measuring, after integration, I get different values depending on the sampling step. This can not be true, since I am measuring in one and the same wavelength range, and changing the step (measurements for every 10 or 50 nanometers) should not affect the final result. I think the problem is in the method of intergration. Is someone familiar with the mathematical integration, or the integration VIs in the Full version of LabView? Can someone suggest me maybe another integration VI? Or maybe a different method. I will be much thankful!
Best regards,
G.
Solved! Go to Solution.
07-12-2016 07:44 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
You should study the method of numerical integration. Regardless of the method used (rectangle rule, trapezoidal rule, Simpson's rule, etc.), the dt input of the algorithm (in your case the integrate VI) has to be synchronized with the sampling step used to sample the waveform. Therefore changing the sampling step and leaving the dt input unaltered gives different results.
Regards,
Adam
07-12-2016 08:19 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Dear Adam,
Thank you so much for the insight you just shared! I am trying to study the method, but my maths are somewhere back into the school grades. x.x
Since the dt is the partition of area that is taken upon integration into the integral, the smallest it is, the most accurate the inegral shall be. However, I can't somehow put into place the sampling step in this case. So... in my case, when I was using the 0.1 dt in the integration VI, and at the same time a step of 50 nm, I had the most accurate result, compared to same measurement, but with more sophisticated power meter that was doing all by itself. While, when I decreased the step to 10 nm, using the same dt of 0.1, gave a huge discrepency.
I will read a bit more of integration, and especially about the few methods that this VI allows, and try to find a solution. If not, you get the best answer anyway! 🙂
Thank you and bests,
G.
07-12-2016 09:03 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
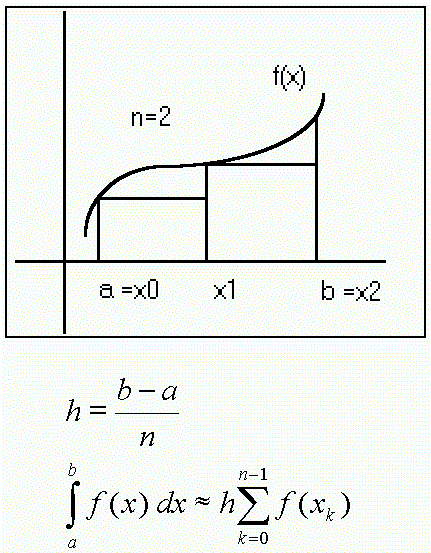
The simplest method of numerical integration is the rectangle rule. The following figure should explain it.
In your case 'h' is the sampling step (in nanometers), as well as the dt input.
Put the case that you have a point every 10 nm, and f(x)=2 constant function. So the area of one rectangle is 10*2=20. Your dt should also be 10. However if you set the dt to 0,1, the formula calculates 0,1*2=0,2 which is a false result. To get the correct value, you would need to have a sample every 0,1 nanometers, so on a 10 nm range the area would be 0,1*2*100=20. Another way is keeping the sample rate on 10 nm and multiplying the f(x) value by 10/0,1=100, so that the are would be 0,1*200=20.
If you are uncertain, just generate a const waveform, and play with the parameters. It is easy to determine the integral of constant and other elementary functionst, like sine or cosine. If you manage to get the correct value on these functions, you should be able to use the same settings on your custom waveform, given it has the same sample step.
I hope it is more clear now
Regards,
Adam
07-13-2016 01:28 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Dear Adam,
Thank you once again very much! I played with the integral values, and decided to use the dt 10 as you suggested. I will use this formula you provided, and will try to make the VI a bit more flexible.
Bests,
G.
07-13-2016 07:50 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello again Adam,
I reconfigured the whole VI, and I still get an error.
1. I tried first by fixing the step of obtaining pints to 10 nm, so it gets a value every 10 nm in a specific range. Than I fixed the dt to also 10, yet I got completely wrong result.
2. I was thinking if I shall also include the units for the nm? Or the unit of the miliwatt... 10^-3?
3. I was typically testing in the range from 200 to 900 nm, but how the range is affecting the final result?
4. In the end I tried to include the formula for h you gave me, but still I get some bizare results.
I am getting more lost... 😞 and it's elementary maths x.x 🙂
07-13-2016 09:12 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
The beginning and the end of the range shouldn't affect the result, only it's width matters.
The units are more important. You have to find out, what physical quantity (and unit) you expect as result.
For example if you would like to get watts, you need to integrate watts/nm on a nm range.
You can check the result easily, supposed you have a constant function, since integrating a constant on a finite range is a simple multiplication.
Another issue might occur. Integrating algorithms (except rectangle rule) use previous points in their formulas to determine the current point's value. The trapezoidal rule for example uses the current point and one previous point, to fit a 1st order curve. Higher order algorithms fit higher order curves, so they use more previous points. However in the beginning of the array of your points, you lack these previous points and this causes accuracy errors.
In case of large amount of data these errors are minimal, but if you have just a few points, they can be significant. An algorithm that uses lower order methods on the first few elements can minimize these errors. I am unsure whether the integrating algorithms in labview offer such functionality.
Still I doubt that this would cause your problem.
Regards,
Adam
07-14-2016 02:08 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Adam,
Well, the range width will change for sure. I had built the app in such a way that you can actually decide if you like to measure values from 200 - 900... or 200 - 400... or go completely in the IR 800 - 1100. The sensor itself is limited from 200 to 1000 so this is the max width.
Units... the machine is measuring in mW... per wavelength. It has inside some value set for sensitivity. I included in my code a formula that devides every measured value to the area of the sensor, and gives each value for each point measured as mW/cm^2... than when all the points are collected in this unit (into an array) than they are being integrated. I am not sure, though if this approach is correct, or I need to divide to the area of the sensor only the final integrated value of the power.
So what I did so far... I am measuring for example 200 - 900 range... with step 10, those are 900 - 200/10 = 70 points. I thought that the dt in the integration VI means the number of the discrete trapezoidal pieces that will be cut from the curve, and used for the integration. I can't understand the logic of my dt being 10 as the step itself. This project is driving me nuts! x.x
07-14-2016 02:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If I remove the initialization of the array shift register, will that feed old values into the integration VI? There are only 4 methods of integratiom, the default one is the Trapezoidal. I am using this method.
07-14-2016 03:08 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
Since numeric integration is addition and multiplication, it does not matter whether you divide then integrate or integrate then divide.
Labview help can also be useful. I copied the following from the help page of 'Numeric Integration VI':
I really don't know what you are doing wrong, you should include your code perhaps.
Regards,
Adam