Remove NaN

[P@Anand]

Thanks now only starting to learn those things. Will this be OK?

[nyp123]

The top of the column, the name of the column

[GerdW]

Hi Anand,

it get's better.

- It would be fine to compare two operations doing the same. As of now you compare your "replace" algorithm with TiTou's "delete" algorithm...

- Updating indicators (like "iteration count") in the tested loops will hurt performance a lot. Don't do that for benchmarking...

- Even now the compiler might be too smart for you. It might "know" your test-array is built from NaNs and might precompile (part of) the loops...

[GerdW]

Hi nyp,

"The top of the column, the name of the colum"

The column name is stored in the header lines, but you delete those lines from your array. Don't do that!

When you need those header line: use them...

[P@Anand]

Looks cool. Learnt a new thing today 🙂

[TiTou]

---

@GerdW wrote:

---

Uf... it's a bit unfair to fill the array with only NaNs... I mean, when I tested my algo I used the kind of data I had, that was arrays between 100k and 2M samples with a max of 10 NaNs for each 100k samples...

[GerdW]

Hi TiTou,

with an array of 1M NaNs your routine needs about twice as long as Anands loop. When you reduce the number of NaNs significantly your loop will be much faster...

[TiTou]

That's what I was expecting.

What I'm wandering now is what happens memory-wise. Is LabVIEW smart enough to do Anands loop inplace?

[Norbert_B]

From looking into the algorithms (and their differences), i would guess that TiTous IS indeed slower than Anands for increasing numbers of NaN's to be replaced.

But i have to point out that with increasing array size, TiTou's will outperform Anands since it reuses memory (works on the original array "in place") whereas Anands create a complete new array.

Norbert

EDIT: Arg, two times misread the code, sorry....

EDIT 2: In order to get proper benchmark results, you have to execute the VI at least two times without unloading it inbetween (and doing other, performance wasting stuff). The first iteration results in incorrect values because of "organization stuff" like allocating memory.

[Mads]

A comment first on the comparison:

You cannot really do the timing-test that way:
 

1. The two methods you are comparing do not do the same job, TiTou is removing the NaN-elements, while you Anand replace them with zeroes.
2. Timing-wise running both methods in parallell will cause them to interfere with eachother.
3. It only tests an extreme case where all the elements are NaNs. 

Now, to the suggested solutions:

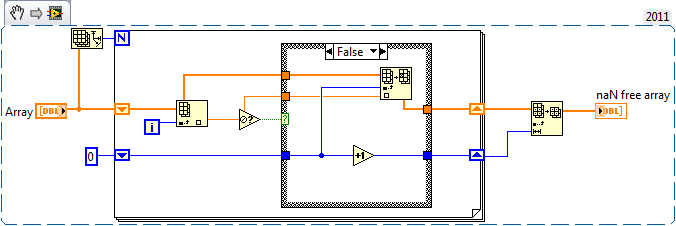
TiTou's solution for NaN removal trades memory for speed by creating what could be a huge array of booleans, and then potentially wastes all that speed (and additional memory) by resizing every time a NaN is found. If the arrays are small and/or contain very few NaNs the penalty is limited, but if that is not the case it can be severe. In general repeated use of any array resizing function should be avoided/minimized.

I have not spent much time on finding an optimal solution (in fact I'm quite sure this is not the optimal one), but the following code would definitely win a comparison test in cases where the task will in fact involve some work (i.e. large array with at least some NaNs):

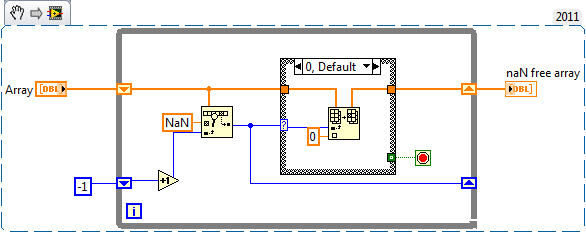
As for replacing NaNs with zeroes Anands code is fine, but yes - using the search function instead of comparing the elements one by one is quicker so a better aproach would be like this: