- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
going deep into timestamp
Solved!01-04-2016 05:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I'm trying to figure out the inside of time stamp raw data for education purpose. I spent some time digging it.
I have read http://www.ni.com/tutorial/7900/en/
I feel the documentation is missing and I would appreciate some help.
Specifically, let’s start with the example in the link above. At the 4th example it says:
|
01/01/2002 00:00:00.000 UTC |
{ 3092601600, 0 } |
I would like to take that 64bit integer that represents the date and time (up to resolution of seconds) and analyze it.
Assume we are dealing with Gregorian calendar (as described in the doc) we have to use 365.2425 days in a year.
So we divide 3092601600 by (365.2425*24*3600) to get the number of years and get 98 and a reminder. So far so good 98+1904 yields 2002 which is the correct year.
The reminder in seconds is 3092601600-98*365.2425*24*3600=20304
Translating 20304 second to HH:MM:SS yields 5:38:24 which is not what I would expect. What am I missing?
In practice it is a bit more complex and I’ll explain it later.
Thanks
Solved! Go to Solution.
01-04-2016 05:51 AM - edited 01-04-2016 05:52 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
01-04-2016 06:12 AM - edited 01-04-2016 06:14 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I think the documentation is wrong (shock horror!). Since you've piqued my interest, I thought I'd have a play...the best way to learn about something is to play with it!
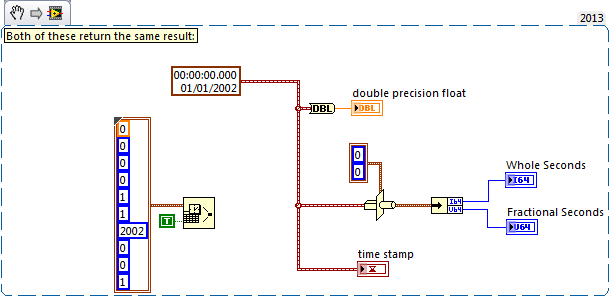
No matter how I try to build the timestamp 01/01/2002 00:00:00.000 UTC, I always get 3092688000 for the number of seconds:
Anyway, the documentation states the I64 part is the number of seconds ignoring leap seconds. Where did you get your value of 365.2425 from? Looking online I found various values (e.g. 365.252222 was one which differs to what you have). I believe this is the source of your issue - the way LabVIEW converts a timestamp to the gregorian calendar is probably fairly sophisticated - taking into account leap days/seconds. If you divide the number by 86400 (seconds in a day), you get exactly 35795 days (exactly) which is correct.
Also note that using quotient and remainder with a floating point input can yield unexpected results (as per the note in documentation) - it is an integer operation.
Plugging the values (LabVIEW epoch and 2002) into an online calculator gives the value of 3,092,688,000 seconds which is what I get in LabVIEW (but differs from the documentation).
01-04-2016 06:20 AM - edited 01-04-2016 06:21 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I think your year length is a problem seeing as leap years are a occasional correction rather than continous. (2002 falls between leap years of 2000 and 2004)
If I am right there is a 98 year span with 25 leap years which means the average length is actually 365.255.
3092601600/(365.2551*24*3600) = 97.99726 years or an error of 236.5 seconds. Possibly leap seconds? Or I am also missing something else.
EDIT: Sam beat me to this but he shows this can't be leap seconds
========
CLA and cRIO Fanatic
My writings on LabVIEW Development are at devs.wiresmithtech.com
01-04-2016 08:19 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The Gregorian Calendar Rules are complicated. We all know about Leap Year (one extra day every 4 years). Some may know about Leap Centuries (which are not Leap Years), and fewer know about Every Four Leap Centuries (which, like 2000, is a Leap Year).
So the average number of days per year, particularly where the time span is very long, is 365 + 1/4 - 1/100 + 1/400 = 365.2425.
However, if we are counting Days since 1 Jan 1904, we can ignore Leap Centuries and Every Four Leap Centuries, as the Leap Year rule for dates after 1 Jan 1904 will follow the "Every 4 year" rule until 2100.
So to get the number of days since Time Zero, divide Whole Seconds by 86400 to get 35795, with zero seconds left over (we should all agree that there should be no seconds left over -- the Calendar doesn't know about "Leap Seconds").
Now for years. Since we are using a date since 1904 and before 2100, the Leap Year Rule is the simpler Julian Rule of Every 4 Years, so divide by 365.25, round down, and get the number of years = 98. Agreement so far?
So what Day of the Year is it? Well, 35795 divided by 1461 (the number of days in a 4-year Leap-Year cycle) gives a remainder of 731, so this is the 731th day of the cycle. Dividing by 365 says this is Day 1 of Year 2. However, Year 1 (1904, 2000, etc.) was a Leap Year, so factoring the fact that Year 1 has 366 days, this is really Day 0 of Year 2, or Jan 1, 2002. Whew, LabVIEW seems to be correct, after all ...
Bob Schor
01-05-2016 07:21 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks all for the responses,
Dear Bob thanks for your precise explanation. NI doc would gain from adding your comments here. As Sam Sharp menssioned the total seconds of 00:00:00 1.1.2002 should be 3092688000 as appose to the doc value.
My time zone is deferent from yours this is why my numbers don’t match Sam’s. Compensating for my time zone and I get the same number.
Thanks for clearing this one.
Shai
01-05-2016 07:24 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for the kind words. I remember puzzling out how LabVIEW Time Stamps worked when I first started using the language ...
Bob Schor