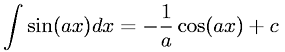- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
how to set or initialize the integration constant in integral x(t).vi
05-16-2011 07:31 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Nitzz wrote:
I think what Jhonsold told is correct. Kindly have a look on the attached VI.
thanx but your vi is not working ....
i am using labview 2009
which version r u guys using... is that an issue??
05-16-2011 07:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
This VI is in 2009
Regards,
Nitzz
(Kudos are always Welcome, Mark as a solution if it is the One;))
05-16-2011 07:50 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hey nitzz .... i dont know wat is the need of all that...
my original vi just works fine wen it comes to extracting the data from the text file and plotting the graph..
my only problem is the integration part...
if anyone could answer my original question: how to correctly integrate the given data
and also how to set the integration constant?
05-16-2011 11:20 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I can't answer your original question "how to correctly integrate the given data and also how to set the integration constant?" but I think I know what the problem is.
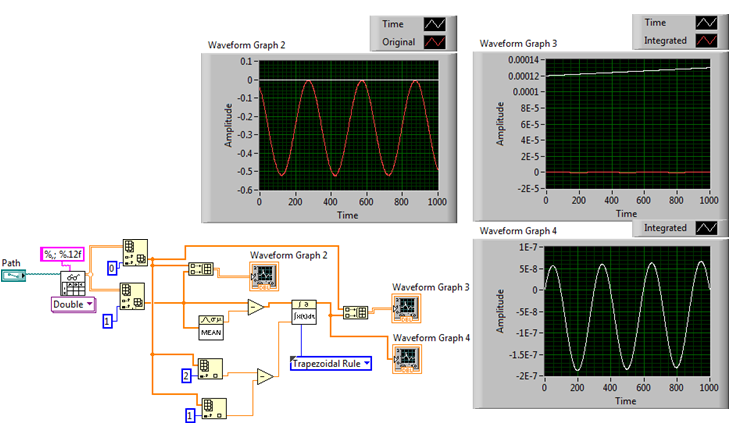
I was able to read and plot your data. The sinewave plotted is negative (except for the peaks which are zero). Integrating the curve calculates the area between the curve and the x-axis. Since your data is always negative, the area is is increasingly negative , thus the squiggly line trailing down. If you calculate and subtract the mean of your sinewave, i.e.. shift its baseline up to zero and then integrate, the result is more like what you expect -cosine.
It's the joy of real world numerical integration versus theoretical mathematical integration. Unfortunately I have to use differential sensors on regular basis, the output of which has to be integrated to be meaningful. I have yet to find a way to perform the integration reliably. Most of my data is impulses so I know approximately what the initial and final condition should be and adjust the baseline accordingly. Scale is a different matter. Numerical integrations will need a scale factor. Once of my sensors includes the scale factor, but most are homemade and the scale factors are derived my measuring known signals and adjusting accordingly.
A couple of comments on your VI. For whatever reasons, most likely regional settings, I had to use johnsold format string or every thing was zero.
Also, you are plotting your Time and Y data against the x-axis, which is samples not time.
05-17-2011 04:46 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hey thanx ctf for the reply....
But how do i calculate the mean of one cycle of the wave??
05-17-2011 08:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
--> But how do i calculate the mean of one cycle of the wave??
I just ran your sample data through the MEAN function. A single cycle is a bit more challenging. Since your sample data is rather clean you can probably extract a single cycle by identifying the mins (or maxs) as the start and end point of a single cycle. Or average the min and max of a cycle. The necessary voodoo will depend on what your actual data is.
I'm not smart enough to answer your original question. In my experience what might work for one dataset is useless on the next and visa versa. The most reliable method I've found is looking at the data and manually adjusting the baseline till it looks 'right', e.g. if the integration tails up shift the baseline of the original waveform down, if the integration tails down, shift the baseline up.
05-17-2011 09:57 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hey i calculated the mean, subtracted it from the data and thus shifted the baseline and then integrated it....
but i am juss gettin a straight line coinciding with the x-axis, ie. 0 ... maybe as u said integrating calculates the area between the curve and the x-axis.. the net area here is zero.... how did u get a -cosine wave??
05-17-2011 11:53 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It's probably not zero, just very small values. Is the integral still plotted on the same graph as your time values? If so the time values expand the Y-axis so the integral is lost in the noise (Graph 3). If you plot the integral by itself you can see it (Gragh 4)
05-18-2011 06:47 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hehe all this while i was getting the integral... but was plotting it wrong..
i should have paid attention to your previous comment on my vi, that am plotting time and voltage against the x-axis..
Anyways.... any idea y after integrating, there is a decrese in the amplitude.... integration shouldnt affect that.. does it??
05-18-2011 12:04 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The scaling comes about because :
The catch is that 'x' is in radians and you never have a frequency such that a single cycle = 2*PI. You have to figure out what 'a' is so that when multiplied by the period/# of points per cycle/frequency/(?) it equals PI (or maybe 2*PI?).