Invert three signals with only two NOT gates

[Andrey_Dmitriev]

Few days ago I've seen nice "breakfast exercise" for the brain in one forum.

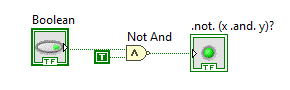
You have three separate booleans, which needs to be inverted, and you have the only two "NOT" primitives available. Also you can use any suitable amount of the "AND" and "OR" logic, but no "XOR" (and bundling into clusters or arrays also not allowed, of course). Start point:

This funny task coming from old school electronic, when engineers trying to use as less inverters as possible. You can easily found an answer in the Internet, but it is quite interesting to solve it (at least was for me).

Good luck!

[LV_Pro]

Playing with NXG it seems!

[altenbach]

---

@Andrey_Dmitriev wrote:

This funny task coming from old school electronic, when engineers trying to use as less inverters as possible.

---

Roy Scheider would have just said "We're gonna need a bigger FPGA". 😄

[altenbach]

I think one is enough 😄

 

[Andrey_Dmitriev]

---

@altenbach wrote:

I think one is enough 😄

---

No, it is still equivalent with three gates (also same with cluster).

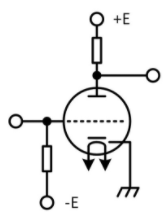
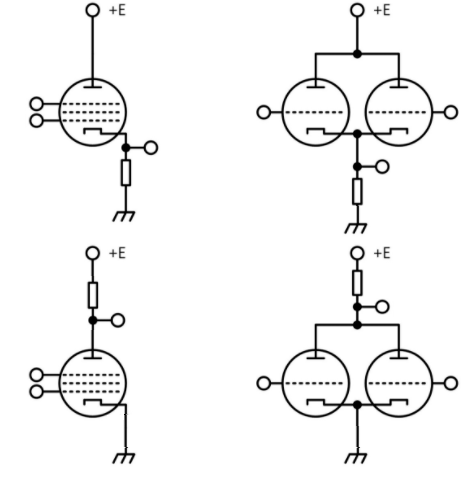
Lets go back to 1952 and build computer.

This is your "AND":

This is "OR":

But this is "NOT":

So, you should spare one expensive triode and replace it with couple of cheap diodes.

[Ben]

I only go back half that far but there is some faint memory that tells me that NOR and NAND gates were used because they were cheaper than the AND and OR gates by a factor of an inverter at the output.

But I would think that in the spirit of the question you would want rule using NAND and NOR gates as well?

Ben

[crossrulz]

---

@Ben wrote:

But I would think that in the spirit of the question you would want rule using NAND and NOR gates as well?

---

A NOR A = NOT(A + A) = NOT(A)

That was simple!

[Andrey_Dmitriev]

---

@crossrulz wrote:

---

@Ben wrote:

But I would think that in the spirit of the question you would want rule using NAND and NOR gates as well?

---

A NOR A = NOT(A + A) = NOT(A)

That was simple!

---

Yes, it is. With NAND it will looks trivial like this:

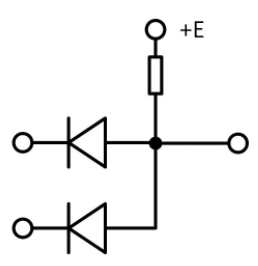
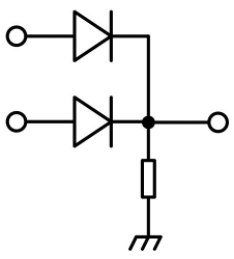
Technically Ben is perfectly right, in the former time AND/OR/NAND/NOR was implemented like this - inversion is just resistors placement:

So, adding inversion to the AND or OR will spare one tube for dedicated inverter. But with Diode logic it was possible to replace tubes with diodes, but not for inversion - here you still need active element (tube or transistor). And our manager said - "save a money - the only two allowed".

[Andrey_Dmitriev]

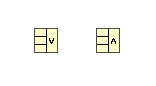
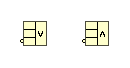
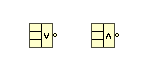
And of course you can use unlimited amount of the compound arithmetic with three or more inputs:

But if you would like to invert input or output, then the only two inversions allowed::

or

[Ben]

I Cheated.... sorta

While I never had to trouble shoot logic gates made from pentodes, I did have to fix ones built from discrete diodes and transistors. That is when I asked "why NOR instead of OR?" which seemed much more simple to understand.

Forgive me if I am wrong but the answer using just two "NOT" and a mix of ANDs and ORs has not been answered?

If I had time I would draw up the Venn diagrams but I have to get in the truck and start a road trip.

Have fun!

Ben