- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Acceleration to derive displacement
02-29-2016 02:26 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
I have posted in the past regarding this problem, but I cannot manage to solve it. I am trying to derive the displacement from double integration of the analog signal. Accelerometer is mounted on a ruler, the ruller bends downwards 50 mm and then allowed to vibrate. Acceleration units are m/s^2 whereas the time is in seconds acquired using 1kHz sampling frequency. The raw signal includes some DC offset.
Initial Speed of ruler = 0
Initial displacement (downwards) = 50 mm
I have tried the following:
- Remove the mean from your sample (now have zero-mean sample-offset).
- Apply low pass filter Butterworth to smooth the signal (Low pass-cut off frequency 150 Hz).
- Integrate once to get velocity using trapezoidal rule.
- Remove the mean from the velocity
- Apply low pass filter Butterworth to smooth the signal.
- Integrate again to get displacement.
- Remove the mean.
The result was not the expected one. I have read something about integrating within the frequency domain for a better representation of the results. How can this actually be done using DIADEM? I have included the results in an excel file.
Thanks.
BradOconnor
03-02-2016 03:01 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
03-03-2016 05:05 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Ulrich,
I have applied a high pass filter in front of the signal to eliminate the drift but this was not effective to proceed with the analysis.
03-03-2016 05:54 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Brad,
Here are my results:
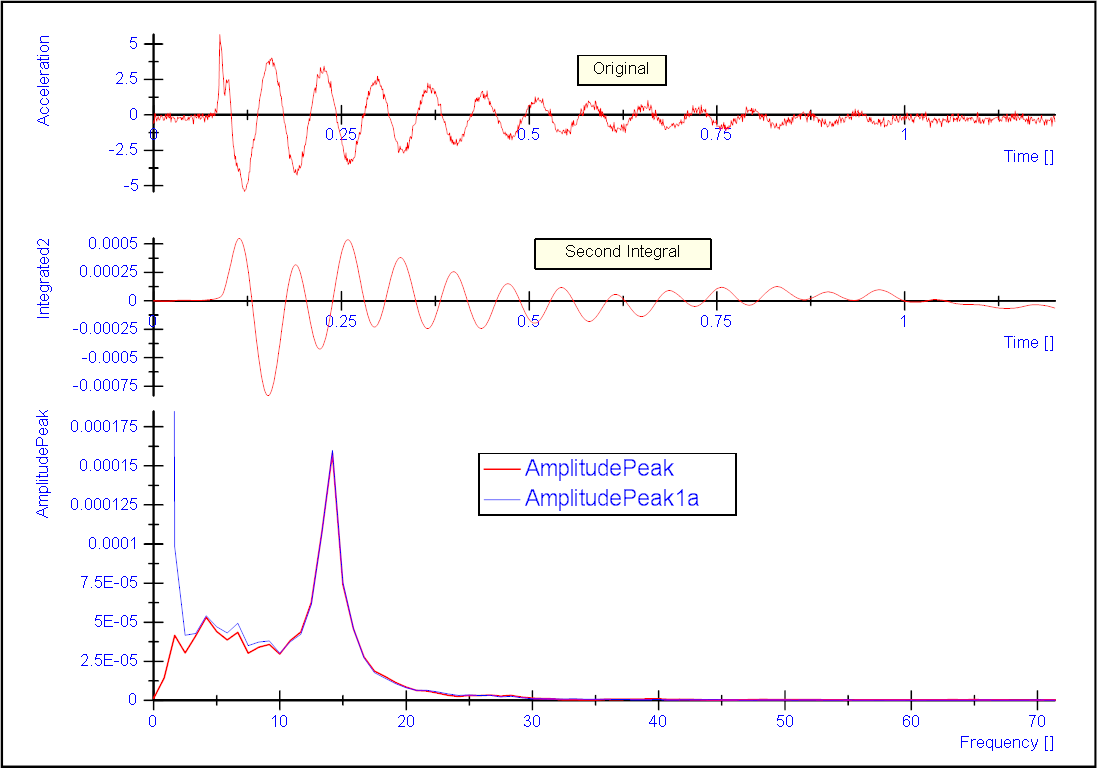
The Integral of the Acceleration signal runs away but the blue line shows, that is also bends. This comes from the drift and can't be eliminated with the offset.
Integral1 shows the integral after the offset is applyed.
Integral2 shows the result after the additional filtering (Bessel, Order 2, Band: 2-150Hz)
The result is still not perfectly alligned, so it might be better with other filters. You need to check different filters and orders to find out what is best for your needs. You also need to look at the phase shift of the filtering. High orders can shift the result and probably there are problems at the begib or end of the result.
Befor you calculate a second integral it might be better to repeat the offset calculation and the filtering.
The offset is still important because the filter is not perfect for offsets at the begin or end of the data.
Here is the recorded script of my calculation:
Option Explicit 'Erzwingt die explizite Deklaration aller Variablen in einem Script.
Call Calculate("Ch(""[1]/Offset"")=Ch(""[1]/Acceleration"")+0.241318936452022",NULL,NULL,"")
Call ChnFiltCalc("[1]/Time","[1]/Offset","/FilteredSignal","IIR","Bessel","Band pass",2,0,2,150,1.2,25,"Hamming",0,0)
Call ChnIntegrate("[1]/Time","[1]/Acceleration","/Integrated","SimpsonRule",0,0,0)
Call ChnIntegrate("[1]/Time","[1]/Offset","/Integrated1","SimpsonRule",0,0,0)
Call ChnIntegrate("[1]/Time","[1]/FilteredSignal","/Integrated2","SimpsonRule",0,0,0)
If this is not, what you are looking for, it might be nessaccary to explain more in detail, what you are looking for.
Ulrich
03-03-2016 02:58 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Ulrich,
Thank you for your reply. I attached a word file with the integration results.
In step 1, acceleration has g units.
In step 2, an offset is applied on the signal (same as yours +0.241318936452022) and the units are changed to m/s^2. I am curious to see how you calculated 0.241318936452022.
In step 3, the FFT is calculated. This shows a frequency roughly 14 Hz. The acquisition runs in a samping frequency of 1 kHz. The max. Frequency band is 1000/2 = 500 Hz.
In step 4, the band pass filter is used as you suggested.
In both step 5 and 6, integration of the filtered signal takes place.
Before to use other filters, the end result for the displacement looks to be very weird. In the second integral calculations, the offset and filtering do not seem to be applied as they alter the graphs.
Bd
03-04-2016 08:04 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
I calculated the arithmetic mean with the statistics function. Thi is shown in the attached script.
In the old example, I did only the first integration. Before the second integration, another offset correction and filtering should be done.
If you are actually interested in the FFT of the second integral, you can do the integration in time domain or in frequency domain. The result should be the same for both calculations.
The Integral of the FFT (in frequency domain) can be calculated with FFT/(Frequency*2*PI).
I have attached a script that is doing two integrations both ways. There is a huge static part below 2Hz in the frequency domain but the FFT of the results is almost identical in the interesting areas:
The blue result is calculated by doing the FFT from the original data without any filtering. After this I calculated the second integral with
AmplitudePeak1a = FFT / ((Frequency*2*PI)^2)
The fact, that the FFTs are that close together shows, that the calculation is correct and if you need the second integral in time domain, this gives more confidence in the offset and filter calculation.
Ulrich Bierwisch
03-04-2016 02:58 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
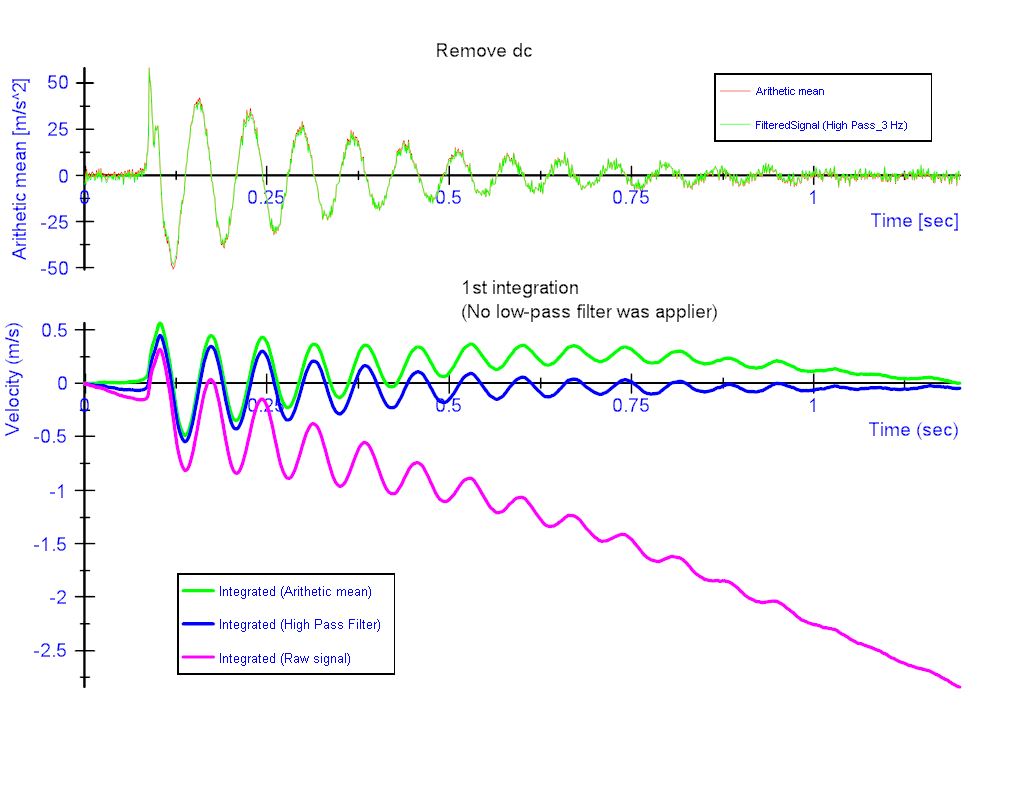
Here are the results I got. It looks that a high pass filter of 3 Hz is more stable compared to the arithmetic mean calculations, but the second integral to calculate the displacement still seems unreasonable.
Brad