- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Algorithm suggestion please.
Solved!05-03-2012 02:33 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi folks,
Can anybody suggest some proper algorithm on this?
I have two input variables and one output data. What will be the most efficient algorithm to figure out the input values that generate peak output?
Thanks.
Solved! Go to Solution.
05-03-2012 04:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Midam,
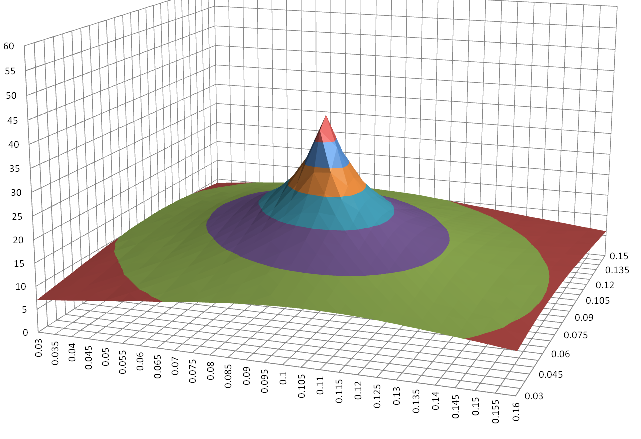
Could you clarify your application? I see you are generating a 3D graph that has a peak. Are you trying to find an algorithm to generate the graph in LabVIEW?
05-03-2012 06:05 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Stephanie,
We have a DUT that has two inputs and one output. The plot is an example of what output (Z) will be like when two inputs (X and Y) are swept.
The inputs that generate peak output will be vary lot to lot. So the aim is to find the X and Y that give peak Z as quickly as possible.
Of course I can get the values if I sweep X and Y like the 3D plot but it requires tremendous measurent time and less productive.
Thanks.
P.S. plotting 3D plot is not the aim.
05-03-2012 07:39 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
This is a standard optimization problem. Will all of your DUTs have a single maximum over the range, or is it possible that there could be multiple local maxima? If there's only one peak, the problem is much simpler. I would start with a web search for "optimization algorithms" or the Wikipedia article for Hill Climbing.
05-03-2012 08:00 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I assume that each xy pair is a measurement you need to take and you want to minimize the number of steps to find the best pair.
any method that uses gradients is probably out because the partial derivatives are not good enough.
i would probably try nelder-mead.
05-03-2012 08:04 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I may be missing something here, but if you have a 3D plot of your data, then you have provided a 2D array of Z values to it, so simply use the Min/Max function to get the location of the maximum:

Of course this will only work if your data is not too noisy, in which case you would have to fit the peak with the appropriate functional form (you could also smooth out the data before looking for the maximum).
05-03-2012 08:14 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Sorry X. I was a little bit unclear.
The aim is getting optimal values without the 3D plot. Getting the data for 3D plot like that is really time consuming task. (long measurement time)
Kudos for those who suggested the algorithms and those are kind of what I wanted. Now I need to dig in these theories.
BTW, when it comes to implementing algorithms, I wonder if there is readily available LabView functions or toolkit? (Trying not to invent the wheel again if that is the case)
Cheers,
08-13-2012 04:12 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Midam,
Have you got the VI for your 2D optimization?
I am looking for a three parameter (xyz scans) optimization VI. If I fix z position, I expect that my xy scan would generate the similar intensity peak as yours. I am thinking about the 3 parameter optimization to speed up the overall search.
Regards.
Fang
08-15-2012 12:06 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Fang,
Yes, I have successfully implemented VI by myself. As accepted solution above, I adopted simple hill climbing algorithm. I 'think' the key requirement is that your 3D surface need to have only one maxima (no local maxima) and there needs to be slopes that can be measured with your measurement resolution.
If you have any doubt, I may suggest you to do XX sweep measurement and have a look how the surface looks like.
Cheers.