- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
All you Math sizes, Here is One For You Revisited
Solved!03-24-2015 02:08 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Inspired by Greg I'll give you all an oportunity to solve my problem for me
Given distance between tracks and normalized forces solve for X, Y and Rho.
Assume I'm writing a simultor for motion of a tracked vechile of some sort
"Should be" isn't "Is" -Jay
Solved! Go to Solution.
03-25-2015 05:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Jeff,
Do you know what this would look like as a mathematical algorithm? I can try and help out with how that’ll look in LabVIEW.
Kevin
03-26-2015 02:34 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I like math problems, but what is "rho"? Since it is a "tracked vehicle", I'm assuming it is not a mis-spelling of "Row, row, row your boat." I'm also unsure that I understand the other parameters (max speed and dt I understand, but not the other three). How does "Rel Vel" (relative velocity? relative to what?) correspond to X and Y (I assume it is a derivative, but am still puzzled by "relative")? Are there other constraints (perhaps having to do with "tracks")?
Bob Schor
03-26-2015 02:46 PM - edited 03-26-2015 02:46 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I assume rho is the angle of direction. What are the forces normalized to? Where are the forces entered? is dt fixed or variable? Where do the control values come from? What are the units? Is this a spacecraft (kMPH is pretty fast!!! :D)?
I guess it does the steering by varying the relative speed to the right and left wheel, so the track width is probably constant over the course, right?
We need significantly more information. In any case, using complex numbers would make things easier.
03-26-2015 03:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
OK, that Max Speed is in Kilometers per hour ![]()
The distance between the tracks will not vary for a given vehicle but there may be many sizes of these vehicles in the future.
Relative velocity is essentially throttle percent where with both Left and Right tracks at 1 (Max Forward thrust) the vehicle will attain max speed and no rotation will be seen
Connversly, with Left =1 and Right =-1 the darn thing will spin in place Clockwise (as seen looking down) and the distance between the tracks defines the circumference the tracks travel along.
Rho, in this case is 0-360 Degrees and is the change in angle from starting position
dT is how long since the last value was calulated and may not be constant (if we can get the RT code optomized well tighten up our control loop)
In all I just want to know how far it went and which way its pointing (Useful information for any vehicle in motion)
Yes its, fairly simple trig but I figured someone up here would have an elegant solution and I'm slinging "more urgently needed" wires.
For a example you could look here
"Should be" isn't "Is" -Jay
03-27-2015 09:48 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
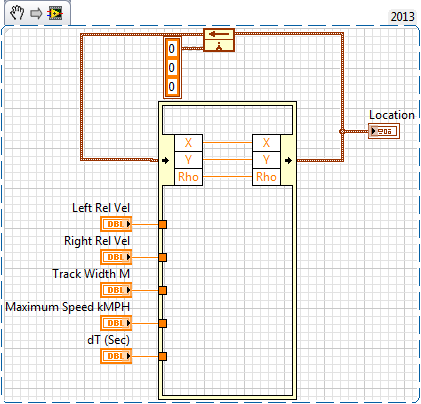
Here's a very quick draft (LabVIEW 2013). Please double-check the math. 😄
(dT is not implemented. A simple solution would be to multiply it with the number going to the N of the FOR loop.)
03-27-2015 10:05 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
Here's a very quick draft (LabVIEW 2013). [...]
That's wonderful! Please add enemies, guns and a scoring system!
03-27-2015 12:09 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Absolutely beatiful code!
At least I was on the right "Basic" math track but bow to my acknwoledged superior in all thinking in complex and multiple coordinate systems at the same time.
"Should be" isn't "Is" -Jay
03-27-2015 02:53 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The first draft had the second element of the state cluster also as complex (speed, direction), but that was dumb because the complex numbers are internally stored in (RE,IM), not (R, theta) of course. This makes it forget the current direction whenever the speed went to zero. Dohh!!!
Would it be better if complex numbers were stored internally as a (R,theta) pair instead? Oh well, too late for that and I am sure it would have other disadvantages.. 😄
03-27-2015 03:38 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Actually, with the exception of the kPH to m/mSec error all I needed to do was change dT to mSec (I get counts anyway) D'Oh and multiply by the delta per ticks.
The real machine is a bit slothful so a 40000 m^2 grid was a bit large.
Again- Much appreciated
"Should be" isn't "Is" -Jay