Bandpass Filter "Ringing"

[CPWhite]

We are using a 4th order Bessel bandpass filter on a signal where we want to measure the level of a 4800Hz signal and suppress any other noise. The low F cutoff is 4500Hz and the high F cutoff is 5100Hz. The sampling frequency is 400,000 samples/sec (which I think is overkill but that's another issue). 

We are testing the presence of a shield on a photodetector by putting the shielded photodetector in a small aluminum enclosure. We energize the enclosure with a 4800Hz sine wave, or turn the sine wave off and measure the background noise level. We then subtract the background value from the 4800Hz "on" value.  We use the RMS value of both signals.

We have an analog 4th order bandpass on an earlier design that does this very well but a new tester design moves the filter into LabView. In the presence of a strong 4800Hz input the Labview filter works fine and gives us a stable signal after a delay. However when the 4800Hz signal on the chamber is off, i.e. the background measurement, we are seeing 'ringing' in the output array of the filter instead of a zero or near zero output. The ringing seems to be excited by transients in the input signal. I input a repetitive 100us pulse instead of the 4800Hz sine wave and the ringing rises and falls following the pulse, with a short delay as expected. This causes out background measurement to be incorrect, or in the case of a very well shielded photodetector, both the background and active signal are unstable so we can't extract a meaningful RMS value. We added a lowpass filter before the bandpass to reduce the high frequency noise and it helped a little but did not eliminate the ringing.

We've also reduced the order of the bandpass filter to 2nd order and it's a little better, but still not the equivalent of the 4th order analog filter which is very stable even in the presence of a lot of external noise. 

One thing we don't understand is the INIT/CONT option on the filter VI. We're not sure from the help file how it should be used in our situation. The help file says "The first time this VI runs or if init/cont is FALSE, LabVIEW initializes the internal states to 0." What internal states? A buffer with all zeroes versus "the final states from the previous call to this instance of this VI when init/cont is true."  The ringing changes a bit depending on whether this is true or false, but not in any meaningful way.

Our process is to capture a few 10s of milliseconds (several hundred 4800Hz cycles worth) with the signal off, measure the RMS value of the output array, then do the same with the signal on, again getting the RMS value. We then execute other tests, then repeat the process with the next photodetector. Since the amplitude of the bandpass output is not stable, we are not getting consistent RMS values and not matching the results with the analog filter. Not at all sure what the RMS measurement VI is doing with an unstable output array. I'll attach some graphical output tomorrow.

[Bob_Schor]

Neither Analog nor Digital filters can "predict the future", so they always work with the "signal Now and in the Immediate Past".  For Analog signals, this situation is continuous -- the "backward-looking window" slides smoothly down the analog data stream.

Digital signals, however, are typically sampled a bunch (bunch -- a technical term for "a constant, but not specified, number") at a time.  You are sampling at 400,000 samples/second, but probably in blocks of at least 1000.  So consider how you'd implement a digital filter -- let's consider a simple form of a low-pass filter, namely replacing each point with the average of the last 100 points.  We'll "wave our hands" a bit about how to start this filter running, but after 100 points, its behavior is clear -- just average the preceding 100 points.  But what happens when we "cross the Bunch boundary"?  Well, when we get the second Bunch, we can still go back 100 points if we use some of the points from the previous Bunch.  We want our (finite) Digital Filter to "look like" it is operating on a Continuous signal as it crosses Bunch boundaries, while the very first, Initial time it runs, we want it to be "unbiased" about the preceding data that it doesn't know.  That's the meaning of Init/Cont.  The usual way this is implemented is to put a Shift Register at the level of this input on the While loop surrounding the Filter call.  Wire "F" to the outside left Shift Register (so that the Filter does the Init Case the first time), and wire "T" to the inside right Shift Register (so it does the Cont Case for all subsequent calls).  See if that makes a difference (it should).

Bob Schor

[Henrik_Volkers]

If you know the frequency you can use the tone detection vi for amplitude ('fit' is constant over timeperiode used and should cover at least 5 better 10 periodes)  or use a heterodyne demodulation or lock-in ...  

Feeding the 10ms snipped into the tone detection vi  (with or without range reduction, see vi help) and compare the amplitude signals should give a nice indicator.

[CPWhite]

Thanks for that summary. I do understand sampling and 'bunches'.

We are not measuring a continuous input. The configuration on the USB6212 DAQ for this analog input is:

16384 finite samples at 400,000 samples/sec or 40.96ms of data. This software was written by a consulting firm and we are having to make a lot of changes and their code is fairly dense and layered (they are using Test Stand which makes things worse IMHO and their own "test wrapper") so we're struggling.

Thanks for your help and it seems to me we should always be using the INIT mode when we call the filter VI, and assuming our 16384 samples = 1 "bunch", leave it in INIT mode.

[CPWhite]

We've seen that VI and there are some nice help files on it, but for downward compatibility in our test systems, we need to use 1 4800Hz 4th order bandpass and the RMS value, not the amplitude. We still may be able to do that with the tone detection VI. I'll check.

[CPWhite]

I've attached  an image with a 10us pulse into our system showing how the bandpass generates 4800Hz that isn't really there, i.e. ringing.

[Kevin_Price]

I draw from a moderate level of knowledge and experience with low and high pass filters, very much less specific experience with band pass and reject filters.  Anything I say is kinda "seat of the pants" thoughts and I gladly defer to those with more expertise.

The envelope of the transient response looks unfamiliar.   The transients I've seen from lowpass filters don't gradually grow and then gradually shrink in response to an impulse.  I don't know if it's a normal phenomenon for bandpass filtering, but figured I'd mention that it looks kinda odd to me.

The fact you're taking short discrete finite bursts of samples can be used to greater advantage.   It will be more *repeatable* to always initialize your filter for the single call on a discrete chunk of data.   With your data (that appears to have near-zero DC offset), it's also probably *good*.  If your data had a large DC offset, things might be different because an initialized filter would see the DC offset as a step function, and your filter output would always include a step response transient.

Since you are post-processing your data chunks, you might consider a different kind of filter.  I don't know a lot of the theory for it, but the "Zero Phase filter" is one I'd be inclined to check out.  (I was in a long-ago discussion where I suggested passing data through a filter once forward and then send the output of that through the same filter in reverse order to "cancel out" the phase delay.  Someone with better knowledge pointed out flaws in that approach and recommended the Zero Phase filter as a better way to accomplish that.  I don't recall details, but think that the biggest reasons focused on the frequency domain characteristics.)

Other ideas might include capturing enough extra "pre trigger" data that the filter transient would have settled out by the time you get to the data you actually need.  Then you can just trim the extra stuff off.

-Kevin P

[CPWhite]

I see what you're saying in terms of "banging" the filter with a transient, one might expect a sharp rise followed by a decay. 

We have tried different configurations of filters but can't afford vary to much from previous designs or the readings won't compare.

We do need to explore where/when the readings are being taken and haven't done that yet. The impulse stimuli as shown in my image is not typical and was a test we did to see if the transients are causing the ringing, and these seemed to show that it did.. We throw away the first 2000 samples (5ms) because we do see the signal rising from 0 to more of a steady state so with the low pass in front of the bandpass we get pretty stable signals, except when they are small (low signal to noise ratio), then we see more instability. However, accuracy is not as important at low signal levels so we could live with that.

Thanks,

[Bob_Schor]

One of the Beauties of LabVIEW (which arises directly from its acronymic expansion, 

Laboratory Virtual Instrument Engineering Workbench, is how easy it is to "do experiments" and "try things out".  So I did.  The following little VI creates the following six Waveforms, based on specified # Samples at a sampling frequency of 400kHz:

1. Sinusoid at 4800 Hz with some additive "noise" (default S/N = 0.1).
2. Waveform 1 filtered by Band-Pass Bessel, 4500 - 5100 Hz.
3. 10 us pulse (amp 1) at 0.01, 0.02, and 0.03 sec.
4. Waveform 3 filtered by Band-Pass Bessel.
5. Waveform 1 + Waveform 3 (just for fun).
6. Waveform 5 filtered by Band-Pass Bessel.

The plots go from the bottom to the top (i.e. Waveform 1 is at the bottom).

Some things to note:

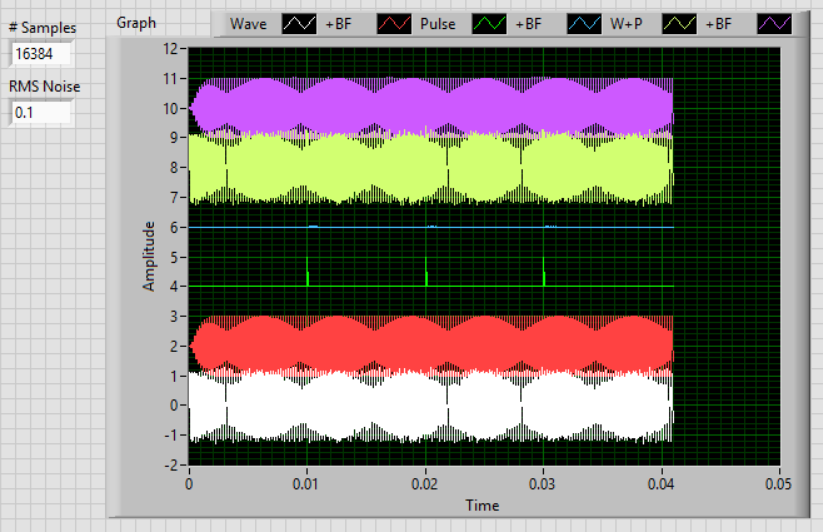
• The Filtered Pulses do produce high-frequency "ringing" around the filter frequency.  If you do a frequency analysis of a square pulse, it will have a lot of high frequency energy, and when you filter it with a Band-Pass frequency, you certainly hope you'll get some data in the frequency range of the Band-Pass, which you do.  Note, however, the size of the signal is markedly reduced (a few % at most).
• Look at the beginning of Waveform 2, the filtered Sinusoid.  Notice how at the beginning, it appears to be truncated ("windowed") relative to the unfiltered signal.  That's due to the "Init" properties of the Filter, which assumes the signal was 0 before t=0 and stepped up to an amplitude of 1 at t=0.  If you were doing a continuous filter, and set "Cont" properly, your subsequent "transitions" would be smoothly combined together.
• If you change the # Samples to, say, 5000, you can get a better view of what's happening, and can better see the effect of the Pulses.  If you increase the RMS noise, you can see that the Filter really does an excellent job.

Bob "Experimenter" Schor

[Bob_Schor]

Note added too late -- I forgot that the original specification called for a 4th-order Bessel Filter.  I forgot to program this in my little Demo (OK, so I'm not an Engineer, I don't necessarily read the Test Specs so carefully ...), so the Front Panel Display shows the result of the default, second-order Bessel Filter.  As you can imagine, it was an Easy Fix to add the Order = 4 input to the three Filters and run it again -- the only "obvious" change is that the additional orders shifted the phase (particularly notable in the residual Filtered Pulses, Plot 4) to the right (as it should).

Bob "Oops" Schor