- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bode plot of experimental data
02-28-2023 06:26 AM - edited 02-28-2023 06:32 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi, I have a black box system with single input and output. I would love the output to follow a more sinusoidal shape. My approach is to identify the system using blackbox's in- and output. I excited the system using consecutives sinusoids from 0.1 to 10 Hz (stepwitdh 0.1).
I divide FFT of output by FFT of input. I feed this into Gain and Phase Margin.VI (Frequency Response).
1: I am not sure about the data to feed into Gain and Phase Margin.VI
Should I use only the data coupled to excitation (0.1 to 10 Hz (stepwitdh 0.1))? So far I use complete bandwith of FFT between 0.1 to user chosen max.
2: The phase plot looks completely wrong. Any hints on that?
02-28-2023 07:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Have you ever taken a class in Signal Theory? In sinusoidal analysis? Or read about it?
The "good news" is that you appear to have a reasonably "clean" system, though there seems to be a noisier-than-I-would-expect "Blue" trace, which I'm assuming is the "input" (or "stimulus") waveform.
You don't want (or need!) the Advanced Signal Processing Toolkit nor the Control Design and Simulation Module for this.
You failed to attach the VIs that showed how you generated the signal used as a stimulus, and explained how you measured/recorded the "blue" and "red" traces you show in the picture "bode.PNG". Here are some steps I'd recommend that you do, but first, let me make some assumptions:
- I assume you have some way to generate a clean sinusoidal signal, with a D/A converter that can output over a ±10V range with at least 12 bit accuracy at a rate of up to 10 kHz.
- I assume you can measure voltages in the ±10V range with at least 12 bit accuracy at a rate of up to 10 kHz, and can record "N Samples, N Channels (specifically 2 channels of 100 samples).
- I assume you have access to an oscilloscope so you can look at the signal you are generating and make sure it is a "clean sinusoid" (not like the blue trace in your figure).
Do a simple experiment. Using an "output frequency" of 1 kHz, generate a ±1V sinusoidal signal (i.e. amplitude of 1V) at 0.1 Hz for 2 seconds (2000 points). Write another routine to sample both the input signal (that you just generated) and the output signal (from your "black box"), sampling at 1 kHz and collecting 2000 points.
Look at the sampled data. You should see two clean "sinusoidal" signals with 20 cycles showing. Just in case you didn't get the signal generating and signal sampling steps perfectly synchronized, you can delete the first 100 and last 100 samples and still have plenty for your analysis. Now think about how you would estimate the gain and phase of the output signal (red trace) relative to the input signal (blue trace).
That's one point on your Bode Plot.
Repeat the above, using higher frequencies of the stimulus waveform in the series 0.1 Hz, 0.2 Hz, 0.5 Hz, 1 Hz, 2 Hz, 5 Hz, 10 Hz, 20 Hz, 50 Hz.
For the last three frequencies, namely 100 Hz, 200 Hz, and 500 Hz, you might want to increase the sampling (and "generating") frequencies from 2 kHz to 10 kHz.
Bob Schor
P.S. -- If I'm "way off base" and you really do know about Signal Theory, and are trying to explore advanced topics like using a chirp stimulus, but are having trouble with the advanced LabVIEW signal processing toolkits, I apologize. Without being able to "look at your code", and largely having only "pictures" (not code) to view, I might have jumped to a faulty assumption ...
02-28-2023 09:50 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If you are going to use FFT analyses to compute frequency response, use this VI:
Your current code does not calculate frequencies correctly. The FFTs you calculate start at 0 Hz (not start f Hz).
More fundamentally, pair your analyses to your stimulus signal.
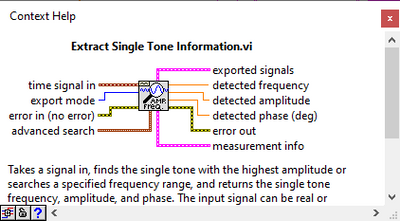
If you need to use a series of discrete sines, then process the subset of the stimulus and response waveforms with a single tone analysis VI such as
However, if you want to use the FFT to look at the broadband response. Hit the DUT with a chirp and use LabVIEW's Frequency Response Function VIs.
Overall, I want to echo Bob Schor's suggestion to design an experiment that you can perform to validate the stimulus, the response, the measurement, etc. Once you have confidence in your measurement process, you can move on to calculation of gain margin and phase margin.
Is your system a real, physical system and you are using analog IO to provide the stimulus and measure the response? or is this a virtual system?
Also, your attached test_binary.txt only appears to have one waveform in it.
NI Sound and Vibration
03-01-2023 07:37 AM - edited 03-01-2023 07:59 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello Mr. Schor
You are right, I never attended a course on this but I followed your advice and did a simple experiment first, see test.PNG
The results look like exptected for me. It is a real system and higher stimulus signals actually don't interest me that much I stimulated the system from 0.01 to 0.5 Hz.
I plotted a Bode diagram according to your advice. In order to figure out the Mag/Phase I multiplied the samples with an exponential, summed them up and divided the results from response and stimulus signal.
For me the Bode plot looks correct, but I am no expert at all.
I upload my code because I also tried to use the mentioned Frequency Response Function (Mag-Phase).vi. The mag looks identical to the solution derived from the exponential, but the phase looks wrong. Any hints on that?
03-01-2023 09:57 PM - edited 03-01-2023 09:58 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If you connect the FGen output directly to the Scope inputs, do you still have all the noise and offset on both stimulus and response such as those in Bode.PNG?
What does your data look like before the detrending VI? Can you remove the normalization and detrending VIs as I don't know what benefits they provide with your improvised dot product, single-tone measurement, or broadband frequency response.
Could you perhaps save a data file with raw data saved for just a few frequencies (such as 0.1, 0.2, 0.5 Hz)? I can't run your code with dependencies on NI Scope, NI FGen, and access to your DUT, but I could try different processing techniques on your data if you can save the acquired waveforms to file.
On a different note, why the long wait (2000 ms) for processing each block? Post processing can run as fast as your machine can compute.
NI Sound and Vibration