- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Help to accomplish Detrended Fluctuation Analysis (DFA) analysis
Solved!06-06-2015 07:47 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
I am tryting to accomplish one graph DFA of time series.
I have ECG signal, where I got the RR intervals. To accomplish the DFA analysis I need to do:
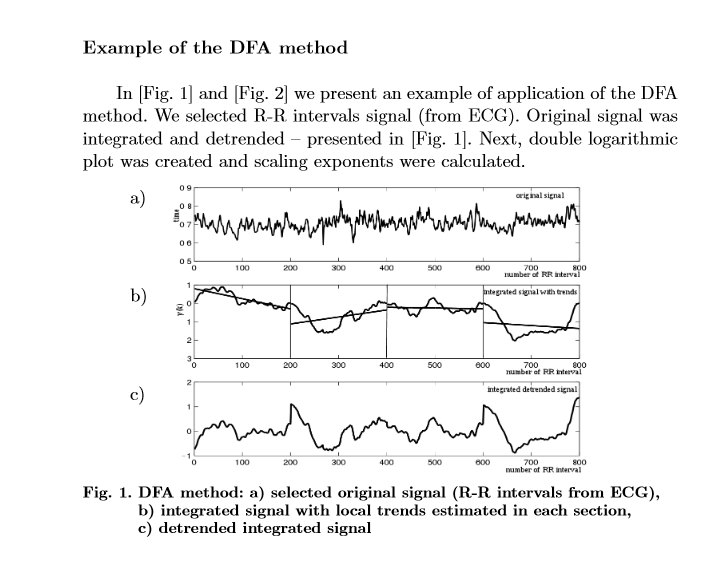
The method of detrended fluctuation analysis has proven useful in revealing the extent of long-range correlations in time series. Briefly, the time series to be analyzed (with N samples) is first integrated. Next, the integrated time series is divided into boxes of equal length, n. In each box of length n, a least squares line is fit to the data (representing the trend in that box). The y coordinate of the straight line segments is denoted by yn(k).
Next, we detrend the integrated time series, y(k), by subtracting the local trend, yn(k), in each box. The root-mean-square fluctuation of this integrated and detrended time series is calculated by
This computation is repeated over all time scales (box sizes) to characterize the relationship between F(n), the average fluctuation, and the box size, n. Typically, F(n) will increase with box size. A linear relationship on a log-log plot indicates the presence of power law (fractal) scaling. Under such conditions, the fluctuations can be characterized by a scaling exponent, the slope of the line relating log F(n) to log n.
In the first step, First, we compute the integrated signal according to the formula
Solved! Go to Solution.
06-06-2015 02:07 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
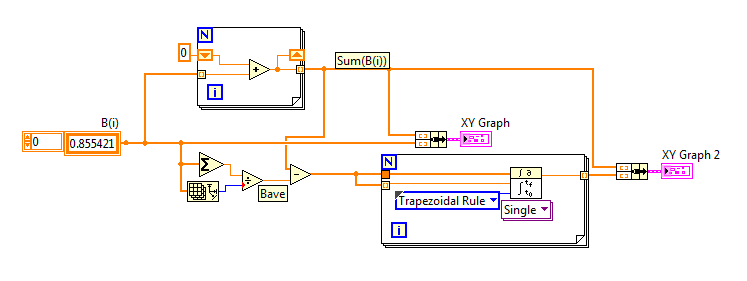
Fred,
Call the input Array in your VI B(i). To the right of B(i), you compute Bave. In the For loop above, you compute Sum(B(i)), and if you subtract Bave from this (instead of subtracting it from B(i), you would get y(k).
Now if you plot B(i) and y(k) on the same graph, you'll see that B is more-or-less flat, and y is more-or-less linearly increasing. This is why you "detrend" y. Here's one way to detrend --
- Pick the "box length", n.
- Reshape y(k) into a 2D array having n rows and as many columns as "fits".
- Create a 1D array of X values corresponding to the column count. The easiest way to do this is to wire the number of columns to a For loop and pass the index, "i", out, converting it to a 1D array of Dbl.
- Pass the 2D array into a For loop, which will work on a row-at-a-time. Also pass in (through a tunnel) the array of columns (step 3).
- Use the Linear Fit function from the Math sub-palette to get the best linear fit from the block of y data. Subtract this fit from the input y array.
- Pass this out of the For loop, making the output tunnel be a "Concatenating" tunnel (rather than the default Indexing tunnel). This gives you back the original, now transformed, detrended 1D array for box length n.
I'm not sure what you do with these data. It seems that you need to do this for many (all?) values of n, but you would be the better judge of this.
Here is a graph of your original data (white) and the detrended data (red) with a box length of 10.
Bob Schor
06-08-2015 06:26 AM - edited 06-08-2015 06:27 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Bob,
Thanks for reply and sorry por late answer!
Ok, if I undertand well, you mean I need to subtract the sum(B(i)). But I dont understand if I need only to substract or I need do the numerical integration.
In the first step it would be:
The bottom graph would be y(k), correct?.
The rest of parts, I think in part 5 I dont have clear. The graph should look so:
The graph you send me, i seems like integrated signal with trends
Can you show me the vi?, please.
Thanks for help!.
Fred
06-08-2015 11:14 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I made a mistake in my earlier code -- I didn't subtract the mean Bave from the integrand (sum) being developed to create y(k), so my y(k) had a definite "trend". I fixed it here.
I noticed you referenced the LabVIEW Biomedical Toolkit -- are you trying to duplicate their DFA code?
I think where you (or, perhaps, where I) went astray was when "integration" is mentioned. I believe this simply refers to the summation step that produces y(k) -- I don't think there is any need for another explicit integration.
Give this a try --
Bob Schor
06-08-2015 12:32 PM - edited 06-08-2015 12:49 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you so much Bob,
Yes, now I got it.
Yes, I want duplicate the DFA graph of biomedical. I checked it but this feature is no open.
Yes, I think you are right and the integration is not requested.
The root-mean-square fluctuation of this integrated and detrended time series is calculated by
This computation is repeated over all time scales (box sizes) to characterize the relationship between F(n), the average fluctuation, and the box size, n. Typically, F(n) will increase with box size. A linear relationship on a log-log plot indicates the presence of power law (fractal) scaling. Under such conditions, the fluctuations can be characterized by a scaling exponent, the slope of the line relating log F(n) to log n.
We have the y(k)- yn(k). For get the F(n). 1/N = n box length?. It lacks the root-mean-square and TWO SQUARED.
For finally, log F(n) o log n.
06-08-2015 12:59 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
The root-mean-square fluctuation of this integrated and detrended time series is calculated by
This computation is repeated over all time scales (box sizes) to characterize the relationship between F(n), the average fluctuation, and the box size, n. Typically, F(n) will increase with box size. A linear relationship on a log-log plot indicates the presence of power law (fractal) scaling. Under such conditions, the fluctuations can be characterized by a scaling exponent, the slope of the line relating log F(n) to log n.
We have the y(k)- yn(k). For get the F(n). 1/N = n box length?. It lacks the root-mean-square and TWO SQUARED.
For finally, log F(n) o log n.
I believe that N is the number of points in the Y series. F is a function of box length, "n", based on a set of "N" data points. Note that N is not necessarily the size of your data array, it is the number of points that went into calculating the particular value of F(n). For example, assume you have 250 points, and you set n = 10. You will divide your points into 25 groups of 10 points, compute y(k) and y10(k) for all 250 points and take the RMS. Now consider n=100. You only have 2 sets of 100 points, so here N = 2*100 = 200, not 250.
Bob Schor
06-10-2015 02:54 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Bob,
Yes, It seems N is the values x1 and x2 boxes for select number of samples, in DFA biomedical, yo can see in attached image, they use from 10 to 40 samples and for x2= 70 to 300 samples.
I dont understand how they decide what value to use and how get the correct values of log n.
I attached the graph that we would get with the current data input, using the 2000 readings beats.
I tried but I dont have it clear. Any advise more?.
Thanks for your time.
Fred
08-24-2015 03:26 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
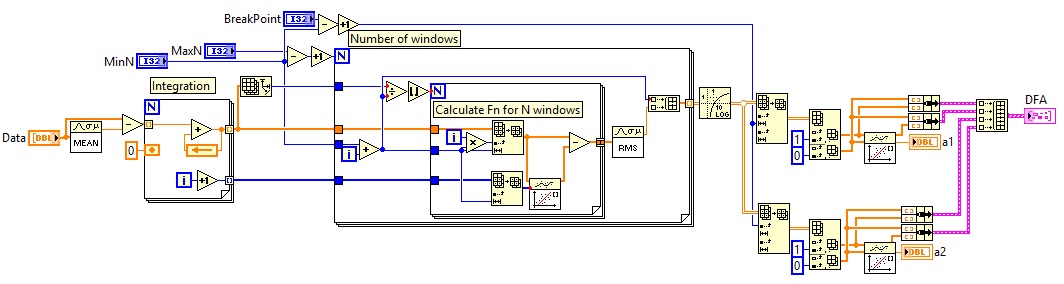
Hi, DFA fustrated me for a long time. My issue was repeating the box segment analyisis for each window in the series. Meaning that if there are 300 beats then the 4 beat interval is repaeted 75 times whilst the 64 beat segment is repeated 4 times with the RMS for each window length being F(n). See my solution below. MinN and MaxN are the minimum and maximum window lengths.
This is able to repoduce the same result as Kubios for the DFA.
Hope this is of some use.
Cheers
Kevin.
08-24-2015 08:44 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Kevin,
Thank you so much!!. I was crazy with this, some weeks ago I tried again but I didnt get the way to do... Now I see correctly.
I attached one example compare kubios and your vi and works fine.
I only see diferent the a1 and a2. In kubios a1 is the higher.
Thank you and regards.
03-03-2016 08:02 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
hi
thanks for information
but sorry i am unable to understand breakpoint significance in this vi. how its value is decided?
kindly help
thanks