- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to get all possible subsets of the elements of an 1D-array
Solved!11-01-2016 12:53 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
I work with spectroscopy and I have 9 different neutral filters (ranging from 10% to 90% in step of 10% of transmission) and I can combine up to 4 different filters in order to get different values of light output power.
For example, if I combine a 10% filter with a 20% filter, I will have light output of 2% (10%*20%). If I combine 10% with 80% and 90%, I will have output of 7.2% (10%*80%*90%), and so on...
Since I have 9 different filters, there are 132 possible ways of getting up-to-four filters combinations. It is cumbersome to determine all possible combinations and associate them with their corresponding output values.
Since I am developing a LabView program for light intensity acquisition, I would like that the program tells me both the combination of filters and the output of the combination (following an increasing sequence of transmission percentage for plotting purposes) before each measurement I perform.
I could do this task in python, as can be seen in the attached python code.
However, I need to do the same in my laboratory LabView 7.1. I struggled a lot, but couldn't develop such program. Can anybody help me, please?
Solved! Go to Solution.
11-01-2016 01:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It seems to me that the problem is equivalent to the following: Using the numbers 1 .. 9, produce all 4-digit numbers where each digit is larger than the one on its left. Thus the first would be 1234, the last would be 6789. Once you have a number, you use the digits to return you the proper filter (1 .. 9) until your set of four is assembled.
I often approach problems like these using recursion (which LabVIEW supports by allowing you to create a re-entrant VI). To generate a 4-digit number with each digit being "bigger" up to 9, generate all 4-digit numbers that start with 1 and "follow the rules" and all that start with 2 and "follow the rules" and ... and all that start with 9 and "follow the rules". What does it mean "and follow the rules"? Well, for the 4-digit number, it means "Generate a 3 digit number that starts one more than we have to our left .. 9 and followed by a 2-digit number that follows the rules". This is the same formulation for our 4-digit number, except we have one fewer digit and are given a new starting number. We stop the recursion when we get to the "Generate a 0-digit number" step. Note that as so formulated, I'm allowing "Generate a 4-digit number starting with 9 ...", but that's impossible by the rules, so there are additional "stopping" criteria beside the number of digits, left as an (interesting) exercise for the reader.
I'm going to give this a try, myself, so if you get stuck after a day or so and no-one else has posted a solution, let me know ...
Bob Schor
11-01-2016 01:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
Here's a link to a community post showing how to get all the combinations of an 1D array, given a certain length:
https://decibel.ni.com/content/docs/DOC-15584
Replace the missing "Get Combinations.vi" with "nCr.vi". You can change the array data type and put code in loops to get combinations for 2, 3, and 4 elements all in one VI execution.
Pang
You too can be LabVIEW Awesome!
11-01-2016 03:59 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Well, I'm a little disappointed that a Certified LabVIEW Developer felt compelled to post someone else's solution. I wrote my own recursive VI that takes Array Size (4), First Element (1 if "counting", 0 if using as an Array Index) and Last Element (9 or 8), and returns a 2D array of (in my test case of 9 filters, 4 at a time) 126 x 4 elements (note that the Binomial Coefficient, "9 choose 4", is 126). I'm going to wait a bit before posting just in case some of you decide to try your hand at recursion.
Bob Schor
11-01-2016 04:51 PM - edited 11-02-2016 01:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Bob_Schor wrote:Well, I'm a little disappointed that a Certified LabVIEW Developer felt compelled to post someone else's solution.
I don't think it is the correct solution. While each filter can only be used at most once, the "no filter" can be used up to 4 times, occupying up to four slots. The total number of possible combinations is the sum of (no filter, 9 chose 1, 9 chose 2, 9 chose 3, 9 chose 4). Seems like 256 possible selections but then we need to eliminate duplicates.
11-02-2016 02:16 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi, Bob. Thank you for your quick reply.
Actually the problem is a bit more complex, because one of the filters can break at any time (if someone lets it fall on the floor, for instance). It is common to break filters, since they are fragile (and we just order new ones whenever necessary). Therefore, I need LabView to tell me all possible combinations of the "N" filters that I have available (LabView input: filters; LabView output: combinations of up-to-four filters among the ones I have available.).
Regards.
11-02-2016 02:18 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi, Pangvady. It seems to be one good solution for me. I will try it. Thank you very much.
Would you have any alternative?
11-02-2016 03:08 PM - edited 11-02-2016 03:13 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
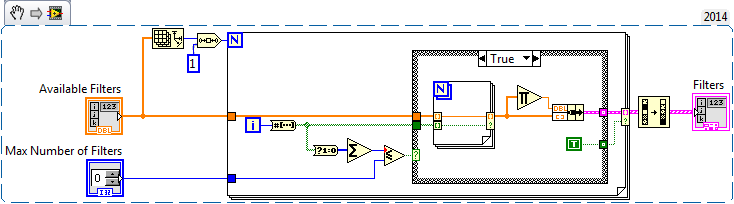
I tend use a simple boolean flag to describe if a given element (filter) is included or not. If you have less than 2^31 filters then it is easy to use the I32 loop counter to iterate through the combinations.
I convert the counter to a boolean array and check that the number of true values is less than or equal to the maximum number of filters allowed. If so I record the values corresponding to the true bits. In this case it is fortuitous that Multiply Array Elements returns 1 for an empty array, exactly what is needed here so the no filter case gives you 1 automatically.
I realized too late that you use LV7.1 so you will have to convert the inner loop using conditional tunnels to the old-fashioned way.
11-02-2016 03:39 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Maybe I'm mistaken, but I think Darin meant if you have at most 32 filters, as he is cleverly encoding "Use Filter i if bit i = 1", so in a 32-bit number, you can represent 32 filters.
In your case, you have 9 filters, so there are 2^9 (or 512) possible combinations, from all zeros (no filters) to all ones (all filters). You can use Darin's "counting" method to enumerate the values of each filter combination. You'll probably find that there will be "clashes", more than one filter combination that gives you a particular density, and you may want to (for practical reasons) limit yourself to a "maximum of 5" (or 3, or whatever), in which case you make another pass and exclude filters whose "index sum" (the number of bits in their position) is too large.
Best of all, if you keep the LabVIEW program around, when you drop and break Filter 4, you just adjust the filters to 1, 2, 3, 5, 6, 7, 8, 9 and run the program again, getting a new list of Filter Combinations.
Bob Schor
11-02-2016 03:50 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Bob_Schor wrote:Maybe I'm mistaken, but I think Darin meant if you have at most 32 filters, as he is cleverly encoding "Use Filter i if bit i = 1", so in a 32-bit number, you can represent 32 filters.
Oops, was actually thinking of 2^31 combinations, or 31 filters. I32 instead of U32 as the counter costs you 1 bit. Thanks.