- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to understand the relationship between the frequency character and the system 's nonparametric estimation?
Solved!07-15-2016 11:39 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello:
I am in program about system identification. The process is as below:
Firstly, I use a sweeping sine signal (the frequency range is from 0 to 50 Hz) to stimulate the actuator;
Secondly, , I use a lowpass filter( the cutoff frequence is 45 Hz) to filter the response signal, as the picture below;
![Y]1)BZO6Y9HC6)Z`KKK}SRK.png Y]1)BZO6Y9HC6)Z`KKK}SRK.png](https://forums.ni.com/t5/image/serverpage/image-id/186253i453E0BB49043355C/image-size/original?v=v2&px=-1)
As I use a signal filtered by a lowpass filter with a 45Hz cutoff frequence, the magnitude reaponse of the nonparametric system surely should also be cut off in 45 Hz, which means the magnitude of high frequence exceeding 45 Hz should be very small. Am I right?
But the truth is ,as the picture below:
So, my questions are:
How to explain this result,?
Why does the magnitude response first be cut off as my guess, but then rise up in the high frequency range?
How to solve the problem?
Any assistance is helpful and welcome.
Thank you!
Solved! Go to Solution.
07-16-2016 06:21 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
To help us provide assistance, please attach your actual VI, not a picture of part of your VI. With a picture, we cannot visualize what isn't shown, and, more important, we cannot execute your code to better understand what it is doing.
Since I cannot see the beginning of your code, I can't tell the origin of the signal you are trying to analyze. Something you could try to debug this yourself is to use a known signal -- build a system that (for example) "does nothing", which can be modelled as a Gain of 1 system. Do you get a Gain of 1 and Phase of 0? Building a Low Pass filter is also easy (a Moving Average) -- does it give the expected Low Pass response?
Bob Schor
07-16-2016 07:24 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
To help isolate the problem plot the output of the filter directly. Does it roll off and stay low in the higher frequencies? What does the input to the filter look like? In particular what does its high frequency spectrum look like? How fast do you sweep the sine signal?
What is the behavior of the Nonparametric Estimation VI with a near zero input over a wide frequency range? (I do not have the SI toolkit so cannot look at it).
The low frequency portion of the system response appears to have two sharp resonances, one at ~7 Hz and the other possibly at the third harmonic ~21 Hz. From the appearance of the graph I would guess that you do not have enough data near those resonances to adeqautely characterize them. Sweep more slowly and take a lot more datapoints.
Lynn
07-17-2016 06:03 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for your assistance, ![]()
I did what you told to me today, and still the problem was the same.
Maybe I did not describe my problems clearly, here I give a decription again with more details.
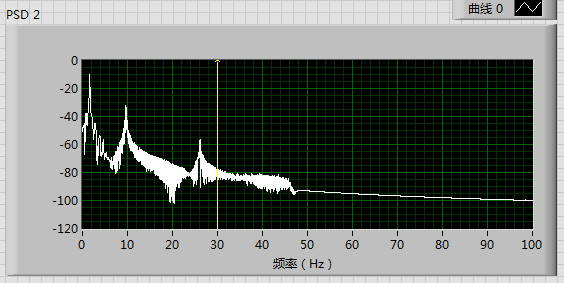
I use a sweep sine signal (0—50Hz) to stimulate a structure, and the response signal after being filtered by a lowpass filter (the cutoff frequence is 45Hz), is as the picture below
We can claerly notice that the first three modal frequences of the system are 1.6 Hz. 10Hz and 27Hz respectively. Also,the high frequences exceeding 45Hz have been cut off. That is reasonable.
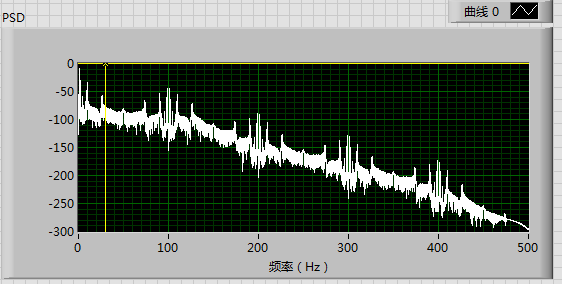
But the problem is ,when I put this filtered response signal into a nonparametric system identification VI with the stimulating sweep sine signal, the frequency character that the nonparametric system identification VI gives is like this:
Yes,we can see the frequency magnitude character that the nonparametric system identification VI gives is only right below 50Hz which is near the cutoff frequence of the lowpass filter. In fact , if you set the cutoff frequence at 100Hz, the frequency magnitude character will also step up at 100Hz as here in 50Hz.
As this is the system that the nonparametric system identification VI gives, when I want to do a parametric system identification, the parametric system identification VI in labview also gives a wrong result, because it will recognise the natural frequences are in the high frequency range.
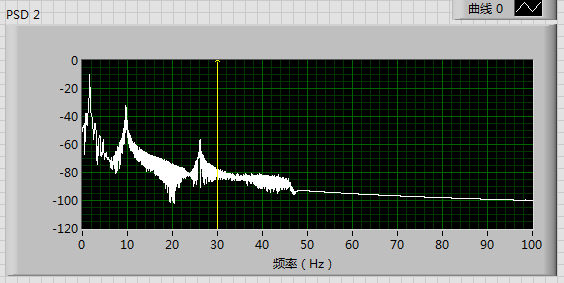
The magnitude character of the system estimated by the parametric system identification VI is as below:
Right? The use of a filtered response signal leads to a wrong result, in my experiment.
Why did I use a filtered response signal?
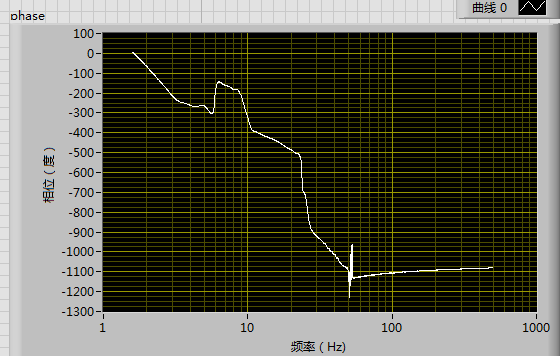
Because the response signal that I get is also wrong in high frequency range without being filtered. Just as the picture below:
I cannot explain what is the reason that the response signal in high frequency range is like this. It seems like being mirrored but also descends.
We can see at 100Hz, the magnitude character is bigger than the true third modal frequence. That affects the estimation of system.
So, please heip me find out the reason and the solution of my problem.
Please.......
Oh, here is my program.
Thank you again.
07-17-2016 06:13 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for your assistance.![]()
I've given another description with more details and also my VI, so ,please look at it again and help me out .
Oh, I did the suggestion that you adviced me to do a longer estimation and use wider range of sweep sine signal, but the result is still unreasonalbe. So ,I have no idea now.........
The problem is THE SYSTEM IDENTIFICATION VI, I think.
But how to solve the problem?
Thank you again .
07-17-2016 08:08 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I do not have the System Identiifcation VI so I cannot see what it does. Does the detailed help desribe how it calculates the response?
If the system response is based on output(f)/input(f), then you would tend to expect a large value for the high frequencies where input(f) is very small.
It may not make any sense to consider the output of System Identiifcation VI at frequencies where you did not supply an input.
Lynn
07-17-2016 09:24 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Sorry,here is my VI and the discription of my problem.
I use a sweep sine signal (0—50Hz) to stimulate a structure, and the response signal after being filtered by a lowpass filter (the cutoff frequence is 45Hz), is as the picture below
We can claerly notice that the first three modal frequences of the system are 1.6 Hz. 10Hz and 27Hz respectively. Also,the high frequences exceeding 45Hz have been cut off. That is reasonable.
But the problem is ,when I put this filtered response signal into a nonparametric system identification VI with the stimulating sweep sine signal, the frequency character that the nonparametric system identification VI gives is like this:
Yes,we can see the frequency magnitude character that the nonparametric system identification VI gives is only right below 50Hz which is near the cutoff frequence of the lowpass filter. In fact , if you set the cutoff frequence at 100Hz, the frequency magnitude character will also step up at 100Hz as here in 50Hz.
As this is the system that the nonparametric system identification VI gives, when I want to do a parametric system identification, the parametric system identification VI in labview also gives a wrong result, because it will recognise the natural frequences are in the high frequency range.
The magnitude character of the system estimated by the parametric system identification VI is as below:
Right? The use of a filtered response signal leads to a wrong result, in my experiment.
Why did I use a filtered response signal?
Because the response signal that I get is also wrong in high frequency range without being filtered. Just as the picture below:
I cannot explain what is the reason that the response signal in high frequency range is like this. It seems like being mirrored but also descends.
We can see at 100Hz, the magnitude character is bigger than the true third modal frequence. That affects the estimation of system.
07-17-2016 09:57 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
You said :"
If the system response is based on output(f)/input(f), then you would tend to expect a large value for the high frequencies where input(f) is very small.
It may not make any sense to consider the output of System Identiifcation VI at frequencies where you did not supply an input."
I just cannot understand why the output value is large for the high frequencies where input(f) is very small, doesn't the identified system's frequency character should be the same with the frequency character of the input signal?
It does make sense to consider the output of System Identiifcation VI at frequencies where I did not supply an input. In fact, I think the input signal as below:
does have its value in high frequency range, only to be a little small, am I right? Can't we consider this to be the magnitude character of the system?
If I am wrong ,how to use only the first three modal frequence to estimate the system's model?
07-19-2016 06:09 AM - edited 07-19-2016 06:11 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
One thing: You don't want the system identifier vi to identify your filter, rigth?
So it migth be a good idea to apply the same filter to both signals ... (the exitation and the response) ...
And guess why the system identification palette also contains a data preprocessing sub palette where the filter (and other vis) affect both traces? 😉
And a small bug hint for NI: At least in my 2012 package the SI Bandpass filter vi for SISO wfrms misses the response signal in connector 😄 (it's in the vi but not on the connector pane)
Henrik
LV since v3.1
“ground” is a convenient fantasy
'˙˙˙˙uıɐƃɐ lɐıp puɐ °06 ǝuoɥd ɹnoʎ uɹnʇ ǝsɐǝld 'ʎɹɐuıƃɐɯı sı pǝlɐıp ǝʌɐɥ noʎ ɹǝqɯnu ǝɥʇ'
07-19-2016 09:28 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for your lovely reply![]()
You mean both the exitation and the response should be filtered right?
I know there are vis specialise in system identification,just like this one below:
but still, the result is similar, like this:
I think maybe it is a bug for the algorithm of the system identification vi, for low response in some frequency range,it may lead to absurd results.![]()
As the algorithem of the estimation vi labview gives:
Maybe in frequency range of low response, the cross-spectral density is big, although in my view, it should be small to be reasonable.
Anyway,thank you again.
greeting from China
Lance.
![KSJ@3LA5]R_(Z4LI9@53W]D.png KSJ@3LA5]R_(Z4LI9@53W]D.png](https://forums.ni.com/t5/image/serverpage/image-id/186252iD4C98F4A2570E4C3/image-size/original?v=v2&px=-1)
![7I{JWMYNN~Z`]7[$NP)PJ0M.png 7I{JWMYNN~Z`]7[$NP)PJ0M.png](https://forums.ni.com/t5/image/serverpage/image-id/186261i1895D6E4607DC92C/image-size/original?v=v2&px=-1)

![L8GEN}V_`}B%2W1]QN$6)DB.png L8GEN}V_`}B%2W1]QN$6)DB.png](https://forums.ni.com/t5/image/serverpage/image-id/186390i3BAB822D185CEFBA/image-size/original?v=v2&px=-1)
![%7H}(PS]WOQM]8(L2SSPU_0.png %7H}(PS]WOQM]8(L2SSPU_0.png](https://forums.ni.com/t5/image/serverpage/image-id/186391i09086328D09A3393/image-size/original?v=v2&px=-1)
![[2C@OB}PWVG6RZ}@{F%]SZH.png [2C@OB}PWVG6RZ}@{F%]SZH.png](https://forums.ni.com/t5/image/serverpage/image-id/186394i1CF4953FA7923C02/image-size/original?v=v2&px=-1)
