- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Lottery Generator
Solved!01-04-2018 02:18 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
Here's a quick version I just made. seems similar, but using the riffle index for simplicity. I am sure that improvements are possible.
Today I learned how to Riffle. I think the only other thing is to move spent out of the While Loop so it doesn't refresh the UI every iteration.
01-04-2018 02:30 PM - edited 01-04-2018 06:54 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@FiveV wrote:
I think the only other thing is to move spent out of the While Loop so it doesn't refresh the UI every iteration.
By default, indicators are not set to "advanced...synchronous display" so the fast loop just updates the transfer buffer of the indicator, while the indicator update (transfer buffer to indicator) occurs asynchronously in the UI thread at a much slower rate. It will probably not slow you down, especially if you have multiple cores. I doubt it will be noticeable unless the rest of the loop code is extremely cheap (not here).
01-04-2018 02:48 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Since you seem to be in a learning mood, here's something completely different :D.
This version uses variant attributes(!) for the database. Since attributes are stored in a red-black tree, searching for a match is much faster (O(logN), vs O(N)). It is easily twice the speed of the previous versions.
See if you can figure out how it works. A great addition to any programmers skill set. 😄
01-04-2018 02:58 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@FiveV wrote:
While I agree on the other points. I think I still need to multiple by 69 to get uniform distribution. See more unoptimized code below 🙂
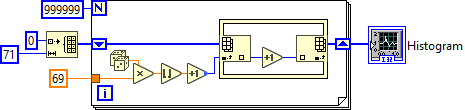
Agreed. Here's a slightly more optimized code to generate the same histogram: (one loop instead of four :D)
01-04-2018 03:07 PM - edited 01-04-2018 03:07 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
Since you seem to be in a learning mood, here's something completely different :D.
This version uses variant attributes(!) for the database. Since attributes are stored in a red-black tree, searching for a match is much faster (O(logN), vs O(N)). It is easily twice the speed of the previous versions.
See if you can figure out how it works. A great addition to any programmers skill set. 😄
You earned a Kuodo for kicking me in the head Christian. The idea of using the Variant Lookup crossed my minds but silly me, I was going to convert the number to string and use that as the attribute name.
Time for an old emoticon...
Ben
01-04-2018 03:15 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
Since you seem to be in a learning mood, here's something completely different :D.
This version uses variant attributes(!) for the database. Since attributes are stored in a red-black tree, searching for a match is much faster (O(logN), vs O(N)). It is easily twice the speed of the previous versions.
See if you can figure out how it works. A great addition to any programmers skill set. 😄
Ok... this is really cool!
01-04-2018 04:15 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Ben wrote:
You earned a Kuodo for kicking me in the head Christian. The idea of using the Variant Lookup crossed my minds but silly me, I was going to convert the number to string and use that as the attribute name.
In my version, the string size is fixed at 6 characters. Any formatted string would be longer, possibly hurting performance.
Yes, attribute names can of course contain non-printable characters. In one of my public programs I cast a long DBL array to a string to be used as key name (see also).
The only limitation is that an attribute name cannot be an empty string.
01-04-2018 07:52 PM - edited 01-04-2018 08:05 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@crossrulz wrote:
4. If you actually need 1 through 69, you need to multiply by 70, round down, and add 1. Likewise, you need to multiply by 27 for the powerball in order to get 1 through 26.
I'm shocked -- Crossrulz is wrong. Consider the U(0,1) random number generator, which generates random numbers between 0 and 1, but less than 1. Multiply this by, say, 69, which makes it a U(0, 69) generator, generating numbers from 0 to 69, but less than 69. If you round down, you get numbers 0, 1, ... 68, and if you increment, you get 1 .. 69.
So the correct multiplier is 69.
But an even simpler way is to round up (also a perfectly good LabVIEW function), which gives you 1..69 in a single step! Simpler.
About 5-6 years ago, I (and a roomful of other attendees) had the pleasure of hearing Darren Nattinger give a talk at NI Week where he threw out LabVIEW Algorithms for common situations at us and challenged us to choose the optimum strategy (we were almost always wrong). His last demo he called "The Texas Lottery Problem", which was generating a random drawing of (I don't remember how many) balls from an urn of (again, I don't remember). He presented 4 algorithms, we all "bet" on the fastest, most of us (including me) guess wrong (he ran the algorithms 5000 times, or something, and we could see which was fastest). However, he did not use a Riffle algorithm (it hadn't been put in the LabVIEW functions yet), and I said "I can do it faster!" (because I knew how to program the Riffle). I sent my solution to him, he admitted mine was faster, but he also "improved" it. I wonder if Riffle came from that exchange ...
Bob Schor
01-04-2018 08:57 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@Bob_Schor wrote:
He presented 4 algorithms, we all "bet" on the fastest, most of us (including me) guess wrong (he ran the algorithms 5000 times, or something, and we could see which was fastest).
I am pretty sure that the riffle solution is not optimal, because it initially operates on all 69 values and we throw most of them away a nanosecond later. I am not planning on writing a faster version in the near future, but I am sure it could be done.
Bob_Schor wrote:
But an even simpler way is to round up (also a perfectly good LabVIEW function), which gives you 1..69 in a single step! Simpler.
The problem her is the wording of the help (e.g. 2015) which states that 0 can actually occur
(Quote: "The number generated is greater than or equal to 0, but less than 1")
If this were true, the "rounding up" solution would have a non-zero probability of creating a zero, because a zero rounded up is still a zero.
As discussed elsewhere long ago, zero cannot occur and we are safe to round up. 😄
01-04-2018 09:40 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
@Bob_Schor wrote:
He presented 4 algorithms, we all "bet" on the fastest, most of us (including me) guess wrong (he ran the algorithms 5000 times, or something, and we could see which was fastest).I am pretty sure that the riffle solution is not optimal, because it initially operates on all 69 values and we throw most of them away a nanosecond later. I am not planning on writing a faster version in the near future, but I am sure it could be done.
You don't use the Riffle Algorithm (as it generates a random orientation of all 69 elements, hence a time on the order of the number of elements, e.g. 69). However, if you run the first, say, 9 initial stages of the Riffle, you'll have your 9 lottery numbers.
Bob Schor