- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Optimizing time spent on numerically solving ODEs?
Solved!07-12-2016 03:37 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Sure. The base equation in questions is the Van Herpe ICU Minimal Model (two compartment insulin-glucose model):
Because there's a max() in dI1/dt, we do need to do some string parsing to decide on the actual F(X,t) that's being used (eg just -n(I1(t)-I_b) + FI/VI.
Additionally, FG and FI are time variant external inputs, so there's some more string parsing that has to be done. Finally, in our implementation of the model, we use a cubic spline interpolation technique to make n, VG, VI, and the constant in front of X(t) in dG/dt time variant. After all is said and done, the only non time-variant string is dX/dt.
The final equations look like this:
Here's the
07-12-2016 04:09 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Sorry, was editing the post with new info when it timed out. Here's the table of constants:
And for initial conditions, you can have G(0) = 200, X(0) = .01, I1(0) = 10, I2(0) = 0
07-12-2016 05:54 PM - edited 07-12-2016 06:06 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Here's a quick python script you can run that uses RK4 on the base model (no time variant parameters, no exogenous inputs):
import time
def max(a,b):
return a if a > b else b
'''
Fourth order Runge-Kutta method in 4 dimensions.
Loops are unrolled from the RKN method for faster execution
'''
def RK4(_G, _X, _I1, _I2, dGdt, dXdt, dI1dt, dI2dt, hs):
_G_1 = dGdt(_G, _X, _I1, _I2)*hs
_X_1 = dXdt(_G, _X, _I1, _I2)*hs
_I1_1 = dI1dt(_G, _X, _I1, _I2)*hs
_I2_1 = dI2dt(_G, _X, _I1, _I2)*hs
_G_k = _G + _G_1*0.5
_X_k = _X + _X_1*0.5
_I1_k = _I1 + _I1_1*0.5
_I2_k = _I2 + _I2_1*0.5
_G_2 = dGdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_X_2 = dXdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I1_2 = dI1dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I2_2 = dI2dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_G_k = _G + _G_2*0.5
_X_k = _X + _X_2*0.5
_I1_k = _I1 + _I1_2*0.5
_I2_k = _I2 + _I2_2*0.5
_G_3 = dGdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_X_3 = dXdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I1_3 = dI1dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I2_3 = dI2dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_G_k = _G + _G_3
_X_k = _X + _X_3
_I1_k = _I1 + _I1_3
_I2_k = _I2 + _I2_3
_G_4 = dGdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_X_4 = dXdt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I1_4 = dI1dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_I2_4 = dI2dt(_G_k, _X_k, _I1_k, _I2_k)*hs
_G = _G + (_G_1 + 2.0*(_G_2 + _G_3) + _G_4)/6.0
_X = _X + (_X_1 + 2.0*(_X_2 + _X_3) + _X_4)/6.0
_I1 = _I1 + (_I1_1 + 2.0*(_I1_2 + _I1_3) + _I1_4)/6.0
_I2 = _I2 + (_I2_1 + 2.0*(_I2_2 + _I2_3) + _I2_4)/6.0
return _G, _X, _I1, _I2
# Exogenous flows would be communicated from LabVIEW, left 0 for now
FG_VG = 0 # mg/dL / min
FI_VI = 0 # uU/mL / min
P1_BASEVALUE = -1.31e-2
P2_BASEVALUE = -1.35e-2
P3_BASEVALUE = 2.90e-6
# Multipliers, varied using spline interpolation in application. Left constant here.
P1_MULT = 1
P2_MULT = 1
P3_MULT = 1
P1 = P1_MULT * P1_BASEVALUE
P2 = P2_MULT * P2_BASEVALUE
P3 = P3_MULT * P3_BASEVALUE
VHM_GB = 100 # mg/dL
VHM_IB = 10 # uU/mL
VHM_ALPHA = 3.11 # 1/min
VHM_H = 136 # mg/dL
VHM_N = .13 # 1/min
VHM_BETA = 1 # min
VHM_GAMMA = 5.36e-3 # ( uU/mL dL/mg ) / min^2
def dGdt(G,X,I1,I2):
return (P1-X)*G-P1*VHM_GB+FG_VG
def dXdt(G,X,I1,I2):
return P2*X+P3*(I1-VHM_IB)
def dI1dt(G,X,I1,I2):
return VHM_ALPHA*max(0,I2)-VHM_N*(I1-VHM_IB)+FI_VI
def dI2dt(G,X,I1,I2):
return VHM_BETA*VHM_GAMMA*(G-VHM_H)-VHM_N*I2
def runVHM():
f = [dGdt, dXdt, dI1dt, dI2dt] # Function pointers
x = [200, .01, 10, 0] # Initial conditions
h = 1 # Time step of 1 minute
__args = x+f+[h]
N = 7200 # number of steps, translates to minutes of simulation with time step of 1.
t0 = time.clock()
for i in range(N):
__args[:4] = RK4(*__args)
''' <- Remove/add a hash before the block comment to toggle this block
# Print solutions array as it comes, reduces performance by up to 100x
print __args[:4]
#'''
t1 = time.clock()
print 'Solution at end time:'
print __args[:4]
print 'Execution time: ' + str(1000*(t1-t0)/N) + 'ms'
runVHM()It's fairly performant when you print solutions as they come, 4ms/iteration, with a massive 400% increase to .01ms/iteration when not printing anything. Although using a Shell Exec call takes anywhere from 100 to 300ms to get the output, so overall using this script would be a loss.
07-14-2016 01:54 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for the equations. I do not know Python so that code is not particularly helpful.
Can you post your VI so I can see how you coded the calls to RK4? That will save me from re-inventing the wheel and probably using different nomenclature. I do not see any definition of the time-varying parameters: V(t), i_s(t), and i_h(t).
Lynn
07-14-2016 02:20 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Those are computed using the Cubic Spline Interpolation VIs; we design a curve, input it and the spline interpolates it. Here's the "core functionality" of the spline interpolation,
Although because of how much code you'd need for me to get individual curves sent, you can just leave those parameters set to 1.
07-14-2016 04:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Attached is (most of) the code you would probably need to look at my architecture. The VI specifically is under VHM/Models/VanHerpeModel/Run Model.vi
07-17-2016 11:16 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Did you get a chance to take a look?
07-19-2016 02:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I started to take a look but have had several interruptions. Multiple power outages due to thuderstorms, and having to do some actual work. I will not have a chance to do much more until Wednesday afternoon or sometime on Thursday.
Lynn
07-19-2016 02:32 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Okay. Please let me know if I need to go into detail on anything within. Documentation is pretty sparse in this code, unfortunately.
07-21-2016 08:11 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
There are several classes missing so it is somewhat difficult to tell how everything fits together. I have a few suggestions although I cannot test them.
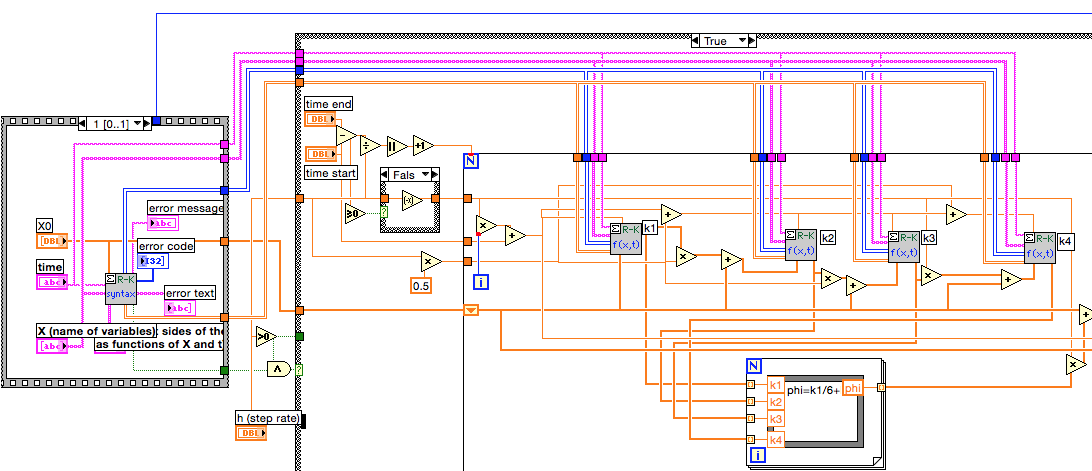
My focus is on the ODE solver using RK. Part of the block diagram is shown below.
Note that the string array X and the time string connect to 5 subVIs. When you look inside those subVIs, exactly the same decoding is done on those strings.
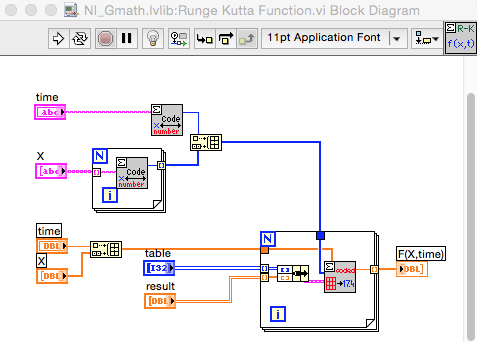
This is the BD of the RK Function.vi. The RK Syntax VI uses the same subVIs.
One suggestion is to create modified copies of the RK VIs which accept the integer arrays rather than strings. This way the strings only need to be converted once per call, or better, only when changed. Furthermore, look closely at the values passed to Decode.vi by your process. If you can do all the calculations on integers as opposed to a combination of strings and integers, it likely will be somewhat faster. Decode appears to process the ASCII values not the numeric values represented by the characters.
The Formula Node in the RK Solver is a factor of 2 slower than the same calculation done with LV primitives for data arrays of 1000 elements or more. The differences are harder to determine for small arrays.
Some of the subVIs have a lot of coercion dots. These appear mostly on different size integers or integer-float conversions so the compiler probably does a pretty good job of eliminating any excess delays. However, I would consider cleaning those up on any subVIs you modify for the other things I have mentioned.
If your data sets are small and the equations converge quickly you may not get much improvement. I think you could see noticeable speed up for large data sets and slow convergence.
Lynn