LabVIEW
Perform operation based in DBL input value
Solved!
Hello,
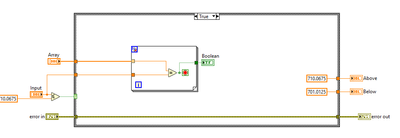
I am trying to perform specific operations based on a DBL input. In my case, if the input is between 701.0125 and 710.0675, I would do Test A. If Test is between 710.0625 and 720.9875, I would perform Test B. If however, the input is either 701.0125, 710.0675 or 720.9875, I would do a test based on those specific values.
I was attempting this, but it is getting convoluted:
Is there an easier method to accomplish this task as the Array ranges grow?
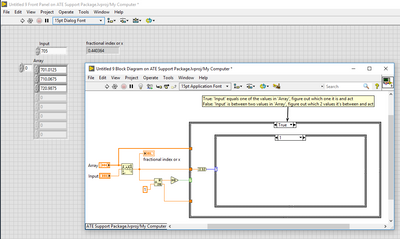
Somehow or another, Threshold 1D Array is going to be your saving grace with something like this. The addition of 'if the value is exactly one of those numbers, then I need to do something different' only makes it a little bit more challenging. This is what I came up with after a couple minutes of thinking about it...
If you aren't already familiar with Threshold 1D Array, start playing around with it and you'll be on your way to a much cleaner solution.
Yes, create a sorted array of limits and use threshold array to convert it into an index.
Have a look at this old example.
(here we use the resulting integer to index into an array of colors, but you can use it for anything else. If you only have one input value, get rid of the FOR loop, of course).
@Brett_Percy wrote:
I would be extremely careful trying to check for exact equality of a floating point value - for your 701.0125, 710.0675 or 720.9875 values, it is very unlikely that any calculated or measured value would precisely equal the constant value in your code.
If you need to match the values to within a certain number of decimal places, either use a range for these as well or convert them into strings first and then match those
I would look at either of these for a more thorough explanation
This one is fairly straightforward
https://www.phys.uconn.edu/~rozman/Courses/P2200_15F/downloads/floating-point-guide-2015-10-15.pdf
This goes into a lot of gory details
https://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html
The TLDR is that binary numbers round differently to decimal ones, so what looks like a short number of decimals can be an arbitrarily long binary number, longer that even extended precision floats can represent accurately
One final thing, is there an overlap in the ranges of your test A and test B cases - so that 710.0600 would fall into both?
Cheers
Brett
To compare floating point numbers to x places, I multiply both numbers by 10^x and round both to the nearest integer, then do the compare. (This also works for rounding to places left of the decimal place as well. Just use negative values for x.)
I have not checked in detail, but it is likely that these values are derived from a fixed-point or raw integer based on a limited amount of bits. It might be possible to do the comparisons on the raw value instead. Of course the question arises about the presence of noise and such. The data would need to be very clean to accurately measure 7 decimal digits accurately and I still believe that the data is quantized to a limited set of steps.
