Problems with data in numeric indicator

[Gabriel1010]

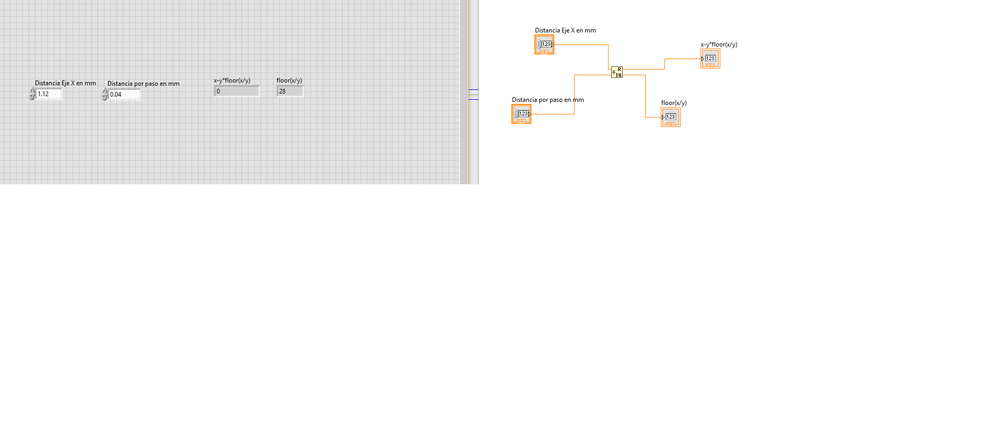
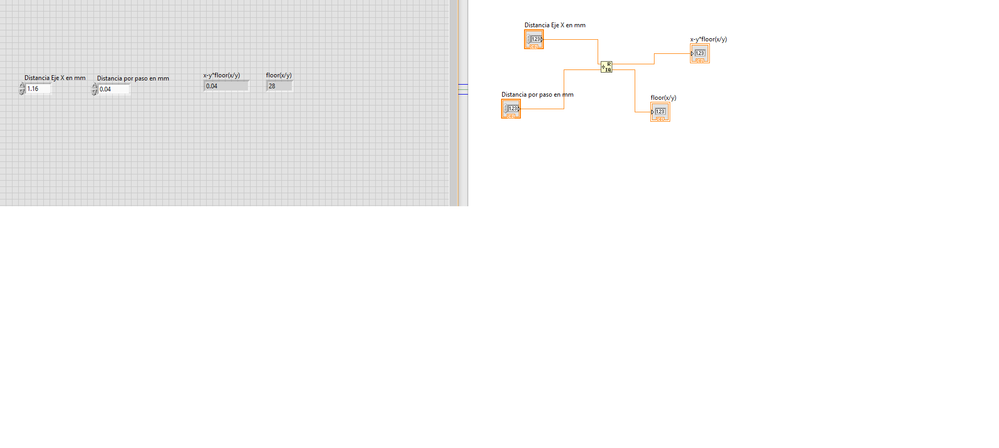
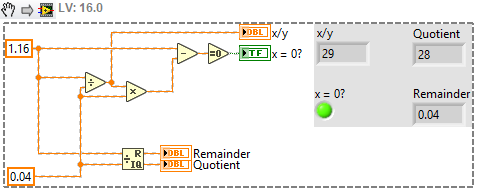
I'm having some issues with the remainder of some operations. For example if i do this operation "1.16/0.04" the remainder in my numeric indicator is 0.04, when must be 0. Because the Quotient of that operation is a whole number as you can see in the image.

Is there an explication of this? If i do 1.12/0.04 the result is correct. Thank you. There's only issues with some operations

[cbutcher]

Probably numerical precision and binary representation.

Check this out as a similar phenomenon:

More helpfully, you can consider doing the calculation yourself. I guess that this rounds in a few extra places...

For more discussion of the double datatype (not specific to LabVIEW) you could read my answer here: StackOverflow link. The question has since been marked as a duplicate, so the other question might have more answers too 🙂

[crossrulz]

Two things wrong here:

1. As cbutcher already stated, Floating Points are not really accurate.  This is a problem with all languages.  The reason being that you cannot put infinite precision in a finite number of bits.  So you will have rounding issues.  The real question is are those errors small enough for you to not care.

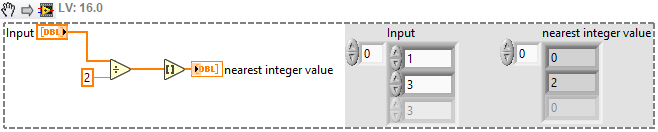
2. The Quotient & Remainder is really meant for integers.  When dealing with floating points, a normal division is almost always what is needed.

[GerdW]

Hi cbutcher,

Check this out as a similar phenomenon

That's no "phenomenon", this is how rounding is defined in IEEE754/854!

It's called "bankers rounding", like described here…

[cbutcher]

---

@GerdW wrote:

Check this out as a similar phenomenon

That's no "phenomenon", this is how rounding is defined in IEEE754/854!

---

Perhaps careless wording!

---

@GerdW wrote:

It's called "bankers rounding", like described here…

---

Thanks for the reminder - it's been a little while since I read through any parts of IEEE754 (or even the wikipedia summary!) and I'd forgotten that the recommended default is half-up, half-down.

I suppose that it's typical (at least for non-computing related fields) to round away from zero, so this is my expected behaviour. I was surprised when I saw the "phenomenon" I highlighted, but as you say, I shouldn't have been!

---

@GerdW

[Gabriel1010]

All right, so anyone knows how to obtain the remainder of those divisions with precision?? I'm working with very small decimal numbers. So i need the remainder..

[GerdW · Accepted solution]

Hi Gabriel,

so anyone knows how to obtain the remainder of those divisions with precision??

Please define the precision you need!

Which numbers are we talking about?

I'm working with very small decimal numbers.

That's bad.

I gets worse when you start to handle numbers with very different values (like ~10^5 compared to 0.001)…

So i need the remainder..

Why?

1.16 \ 0.04

Suggestion: multiply both numbers by 100, round to nearest, convert to integer, then do Q&R…

[Gabriel1010]

it worked well, thank you. I need the remainder because I'm working with a CNC who does 0.04 mm for step. So i need specify the limits of different working zones what need to be multiplys of 0.04mm. So if the working zone is multiply of 0.04 my cnc must stop in that position, if not, I have to specify the range in which I want to stop it. Something like that. But thanks for your support.

[GerdW]

Hi Gabriel,

a CNC who does 0.04 mm for step.

Simple solution: do all your calculations in steps instead of in mm!

This way you can use integers all the way…