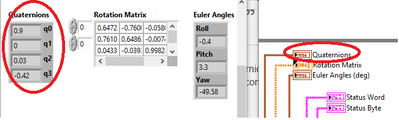
I think that for a full spherical representation, quaternions are much easier to use than Euler angles, once you understand them.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Rotate 3D pictures with IMU
02-24-2023 07:53 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I am reading Quaternions, Rotation matrix, Euler angles and Raw Acc, gyro, mag data from IMU.But I want to use this data in 3D orientation view.
-I cannot use Euler angles directly. Because if the IMU reaches 90 degrees in the Pitch direction, there is a change in the ''roll'' degree.In other words, even if the pitch(X) angle changes to 90 degrees, the Roll(Y) angle must be maintained.
Actually, what I want to tell is to create something like here.
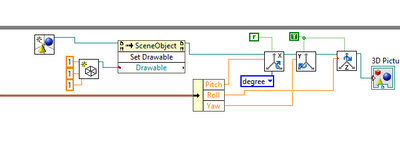
I have a VI that rotates a 3D image like the one below, but I was unable to visualize the rotation according to the IMU movements
-I did some research. It looks like Madgwick filter is being used but I'm not sure.
There is no example that applies the Madgwick filter in labVIEW anyway.
What path should I follow?
Anyone have an idea about this?.
Any opinion given is worthy of respect
02-24-2023 12:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi constructionworker,
From what I can recall, there is an ambiguity in the orientation when using the Euler angles. There is not only one way to handle the ambiguity. You have to handle the ambiguity the way that is specific to your case. If you use quaternion (4 parameters), there is no orientation ambiguity. So, for full spherical orientation, using quaternions is preferable.
There is a Euler angles to quaternion function in the Haro3D library. I would suggest that you simply start using quaternions everywhere in your code. Take your inputs from the IMU and transform right away into quaternions. Within your code, this is where you would handle the ambiguity associated the Euler angles.
02-24-2023 04:00 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you for your answer MarcDub
I think the toolkit you suggested is to calculate Euler angles to quaternion. However, I'm already reading the Quaternion information directly from the IMU with serial communication right now.
But I could not understand how to rotate a 3D object with this Quaternions information.
I think I would understand better if there was an example to give some idea about this.
02-27-2023 03:44 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
|
02-28-2023 02:41 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thanks for your answer, MarcDub
I've done a lot of research and I'm still trying to figure it out.
Based on what you said,
I created something like the following, but according to the quaternion information you provided, the movements are in the opposite direction. Yaw, pitch, roll movements rotate in a mixed way.
What is the solution to this?
02-28-2023 10:09 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I don't understand your problem. There is no defined direction between Yaw, Pitch, Roll and quaternions. For the quaternions, it also depends on the orientation of your rotation axis.
If you want an unambiguous method of dealing with rotation in 3D space, quaternions are the way to go. They are less intuitive but if you pass the initial hurdles, they are quite straightforward.
03-01-2023 08:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
thanks for your answer. MarcDub
Let me explain the problem a little more.
In the example below, it actually works exactly the way I want it to work, except for one thing, it happens to deviations when the pitch 90 approaches.
But I couldn't figure out how to apply Quaternion here.
I checked your previous post here and tried to integrate it into my own application. But I couldn't get the yaw axis rotation here.
if I try to implement ''Rotation matrix'' and use ''rotate object.vi'' should I use a new ''rotate object.vi'' for each axis?
03-01-2023 09:10 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I do not understand your problem. You are only saying that the Euler angles do not work when nearing 90 degrees, and that you do not get the Yaw to work. You don't say what does not work with the Yaw.
Euler angles have a problem when values near 90 or 180 degrees. They work well when your problem is limited to a half sphere.
When you talk about Yaw, Pitch, and roll, it sounds to me that they refer to relative angles (roll is along the fuselage of the airplane for example, just an opinion...). So that would mean that to correctly apply those angles, you need to rotate the coordinate system of the airplane. Just guessing here, since I do not know what your problem is.
So, make sure that you know what you are looking for. Relative or absolute angles (or a combination)? I think that is your actual problem. And then you can decide if you want to use Euler angles or quaternions.
03-01-2023 09:46 AM - edited 03-01-2023 09:49 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It's really my fault I can't explain the problem well.
I want to start over and over.
I read Euler angle, rotation matrix, and quaternion information directly with serial communication.
With this read data, I want the 3D picture to move according to the axis and degree of the IMU.
The ones I tested.
-Example VI in the picture I sent in the previous message. Here he is trying to move the 3D picture with euler angles. But I don't want to use it because of the Gimbal lock problem.
You said you need to use quaternions to bypass the gimbal lock. But I couldn't figure out how to connect quaternions to ''Rotate object.vi'' input. Because ''Rotate object.vi'' has axis(cluster) and Angle(numeric) inputs.
If I need to convert quaternions to "Rotation matrix" and connect X,Y,Z information to "axis" input of "Rotate object.vi", what information should I give to "angle"?
If I use the rotation matrix. The rotation matrix has 3x3=9 elements.
If I convert it to a 2D array and Then convert it to a 1D array. I get 3 pieces of X information, 3 pieces of Y information, 3 pieces of Z information. What reading X value or Y value or Z value should I give to the 'Axis' input. and what data should I bind to the 'Angle' input.
I hope I was able to explain in detail.
I appreciate your trying to help.
03-01-2023 11:02 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Unfortunately, I will not be able to fix your specific problem. I can only try to answer specific questions.
I think that you need to understand what is the information provided by your IMU (absolute or relative angles?, and/or coordinate systems?)
Then going through the angles or quaternions should be trivial. Rotation matrices would work as well but they do not contain more information than the quaternions.
Try things and try to understand the concepts. Once again, if you have a specific question, ask again, and try to back it up with code. Long winded questions without code are time-consuming to answer.