- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
The transfer function of the PID block doesn't show the derivator.
Solved!08-23-2011 07:28 AM - edited 08-23-2011 07:29 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hello,
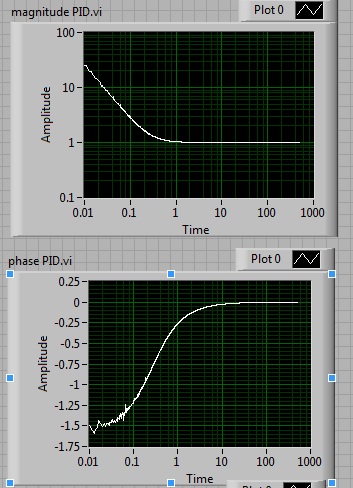
I am trying to use the PID vi, but I when I try the box by itself, it doesn't behave as a "clasic" PID should behave. The main problem is that I don't manage to see the derivator. In the attached vi I compare the transfer function of the PID vi with the transfer function of a PID built by me. My version shows all what a PID should have: integral section (with decreasing magnitude and -90 phase), center area (with constant magnitude and 0 phase), and derivative area (with increasing magnitude and +90 phase).
The PID vi only shows the integral part.
You can also select a step input, and see the output directly. If you choose a large enough derivative time (100 times bigger than the integrator time), and you look closely to the first part of the output, you will see the pick due to the derivator in my version, but not in the PID.vi version.
Does anyone knows what am I doing wrong?
Kind regards,
Pablo Estevez
Solved! Go to Solution.
08-23-2011 08:22 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
by the way, the fall in the phase at the end of the plot of my version of the PID is due to the digital approximation. I am using a sampling frequency of 1kHz, therefore the transfer function looses similarity with the continuous case when approaching 500Hz.
08-23-2011 11:42 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If you swap the Setpoint and Process Variable (so that you have noise in the process variable and a constant 0 setpoint), and also swap the inputs to the initial subtraction in your implementation, you get identical results. My understanding of PID is more practical than theoretical so I can't explain what's happening here, and I don't have time to work out the mathematical differences, but you can open the LabVIEW PID yourself to see what it's doing.
A note about LabVIEW style: there is no need for any sequence structures in your VI. Your code will be cleaner if you remove them.
08-23-2011 02:02 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Dear Nathand,
Thanks for your answer, I tried the change and you are right. That shows that this not a standard PID, since that means (and actually I can see it now by checking inside the vi) that it is not using the derivative of the error but the derivative of the process variable. I know that this is used sometimes to prevent the effect of fast changing set-points, but it is a shame that they do not comment on it in the help, and that this is not a selectable feature. Do you know if there is a way to edit these pre-packaged vi's?
One more question, about the labview style. I included the sequences just to group terms and make the code more readable to separate the integrator from the derivator and not have a knot of entangled signals. Specially when I run the clean-up diagram, it gets very entangled. I have been looking for another way to do that (container boxes, groups). It would be nice if you could suggest me something I can do for it.
Thanks again,
Pablo
08-23-2011 03:15 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
You can modify the PID VIs; make a backup copy first. They live in your LabVIEW directory, under vi.lib\addons\control\pid. They're re-entrant so when you open one from a block diagram you're only opening a clone, which you can't edit; to open and edit the original, open the PID VI, then hit control-m.
I generally try to draw my block diagrams neatly in the first place, and rearrange as they grow to keep them organized. I haven't played with the auto-cleanup tool much. In LabVIEW 2010 you can select a region of the diagram and only clean up that area - maybe that's what you want? If the block diagram cleanup is making your diagrams worse rather than better, you might also want to experiment with the settings for it (Tools -> Options -> Block Diagram). The problem with using sequences for that purpose is that it can make your code perform worse, because you're forcing LabVIEW to execute blocks in a specific order rather than allowing the compiler to determine execution order.
08-23-2011 09:31 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Actually, if you have the LabVIEW PID and Fuzzy Logic Toolkit 2011, we added a output called "gamma" to the advanced PID.
This allows you to define the PID derivative action proportional to the error signal. If you change to 1, it will match the results of the pure derivative.