- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
one matrix subtracted by another gives a scalar?
Solved!08-28-2016 08:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi,
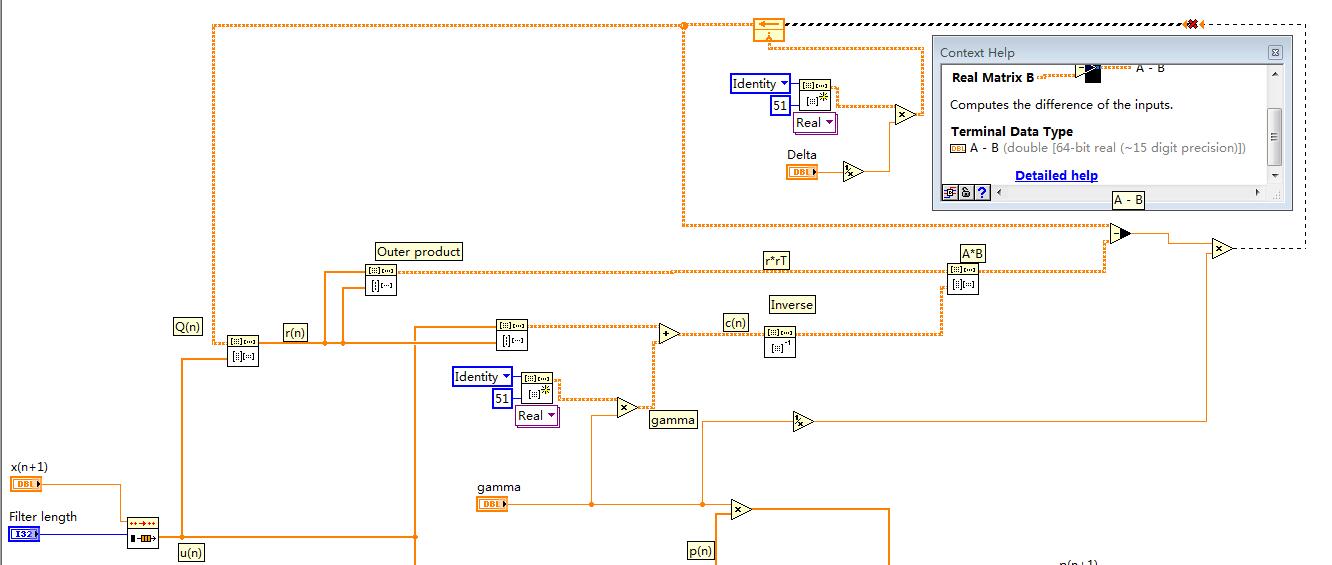
I am implementing an algorithm, Recursive Least Squares Method. Something went wrong with matrix subtraction. That node lays below the context help gives a scalar. It should be a matrix, anyway.
How can I fix it?
Thanks in advance.
Chuan
Solved! Go to Solution.
08-28-2016 09:10 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
For anyone interested in algorithm .
1.Pick 0<gamma<=1, delta>0, m>=0, N>=1
2.Set w=0, p=0, and Q=delta^-1 * I. Here w and p are (m+1)*1 and Q is (m+1)*(m+1)
3. For k=1 to N compute
{
u=[x(k) x(k-1) ... x(k-m)]T
r=Qu
c=gamma+uT r
p=gamma p+d(k) u
Q=1/gamma*(Q-r * rT /c)
w=Q p
}
The errors occured when I was trying to compute (Q-r * rT /c).
08-28-2016 09:30 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
If you want help with your code, you need to supply us with your code. A "picture" that (a) shows only some of the code, (b) is not easy for us to modify (to make it easier to understand what it does), and (c) is not executable doesn't provide enough information for us to really help you.
I can tell you that subtracting two 3x3 matrices gives a 3x3 matrix, not a scalar. So if you are, indeed, doing such a subtraction and getting a scalar, you are probably not doing "what you think you are doing". I'd want to execute (and watch) your code and figure out where you made the mistake, but I need you to attach your VI.
Bob Schor
08-28-2016 09:35 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you!
08-28-2016 09:40 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
What problem is "Recursive Least Squares" supposed to solve? Don't tell me the algorithm, tell me the problem (i.e. "Find the coefficients of an N-degree polynomial that best fits M data points", or something like that).
Bob Schor
08-28-2016 09:46 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
It's to find the best coefficients for an adaptive filter.
08-29-2016 07:44 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
OK, so somehow the Feedback Node messes up Matrix code -- good discovery/observation. Thanks for sending the "simple example". Also, thanks for providing the context for this code.
Bob Schor
08-30-2016 01:34 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Dirichlet,
why did you create another thread for the very same problem?
Why didn't you stick with this thread?
08-30-2016 01:40 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Sorry, I think this one might be too messy and complicated. And I find the problem is just the feedback node.
Best regards,
Chuan