- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bode Plot - issue with phase
Solved!05-13-2015 01:50 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I previously had an implementation issue while trying to produce Bode plots for hardware my team has designed. I have now successfully been able to produce the expected data, with one issue. Some of the phase data points are the reciprocal of what is expected. I will explain the process used...
The hardware I am connecting to allows me to inject signals on channels, as well as stream these channels to my PC application for analysis. The function I am trying to replicate is a frequency sweep, as follows:
- commanding the hardware to override a channel (the stimulus) with a sine wave of given frequency, f
- stream the stimulus channel as well as its response channel for a given number of cycles, P
- perform analysis ("transfer function") on both stimulus and response channels' streamed data
- log the frequency (f) with the corresponding calculated magnitude and phase for use to produce a Bode Plot
- increase frequency (f) and repeat steps
This code sample is the "analysis" performed:
int i, MaxMagIdx, DontCareIdx; double *TimeInMag,
*DontCareArr, TransferReal, TransferImg, TransferMag, TransferPhase, DontCare, AdjFreq; NIComplexNumber *TimeSweepIn, *TimeSweepOut, *FFTSweepIn, *FFTSweepOut; TimeSweepIn = malloc(gSweepCountMax * sizeof(NIComplexNumber)); TimeSweepOut = malloc(gSweepCountMax * sizeof(NIComplexNumber)); FFTSweepIn = malloc(gSweepCountMax * sizeof(NIComplexNumber)); FFTSweepOut = malloc(gSweepCountMax * sizeof(NIComplexNumber)); TimeInMag = malloc(gSweepCountMax * sizeof(double)); DontCareArr = malloc(gSweepCountMax * sizeof(double)); int InputSigIndex; unsigned char OverrideMsg[L_ADC_OVERRIDE_RQ] = {0}; for (i=0;i<gSweepCountMax;i++) { TimeSweepIn[i].real = gSweepInArr[i]; TimeSweepOut[i].real = gSweepOutArr[i]; TimeSweepIn[i].imaginary = 0.0; TimeSweepOut[i].imaginary = 0.0; } CxFFTEx (TimeSweepIn, gSweepCountMax, gSweepCountMax, NULL, FALSE, FFTSweepIn); CxFFTEx (TimeSweepOut, gSweepCountMax, gSweepCountMax, NULL, FALSE, FFTSweepOut); for (i=0;i<gSweepCountMax;i++) { ToPolar (FFTSweepIn[i].real, FFTSweepIn[i].imaginary, &TimeInMag[i], &DontCareArr[i]); } MaxMin1D (TimeInMag, gSweepCountMax, &DontCare, &MaxMagIdx, &DontCare, &DontCareIdx); CxDiv (FFTSweepOut[MaxMagIdx].real, FFTSweepOut[MaxMagIdx].imaginary, FFTSweepIn[MaxMagIdx].real, FFTSweepIn[MaxMagIdx].imaginary, &TransferReal, &TransferImg); ToPolar (TransferReal, TransferImg, &TransferMag, &TransferPhase); TransferMag = 20 * log10 (TransferMag); TransferPhase = RadToDeg (TransferPhase); AdjFreq = (double)((unsigned long)(gSweepFreq*0x200000000/(double)50000000)) * 50000000/(double)0x200000000; fprintf(Logfile_Handle, "%lf\t%lf\t%lf\n", AdjFreq, TransferMag, TransferPhase); free(TimeSweepIn); free(TimeSweepOut); free(FFTSweepIn); free(FFTSweepOut); free(TimeInMag); free(DontCareArr);
It works nearly perfectly. The issue is that the calculated phase will sometimes be positive when it should be negative, and vice versa.
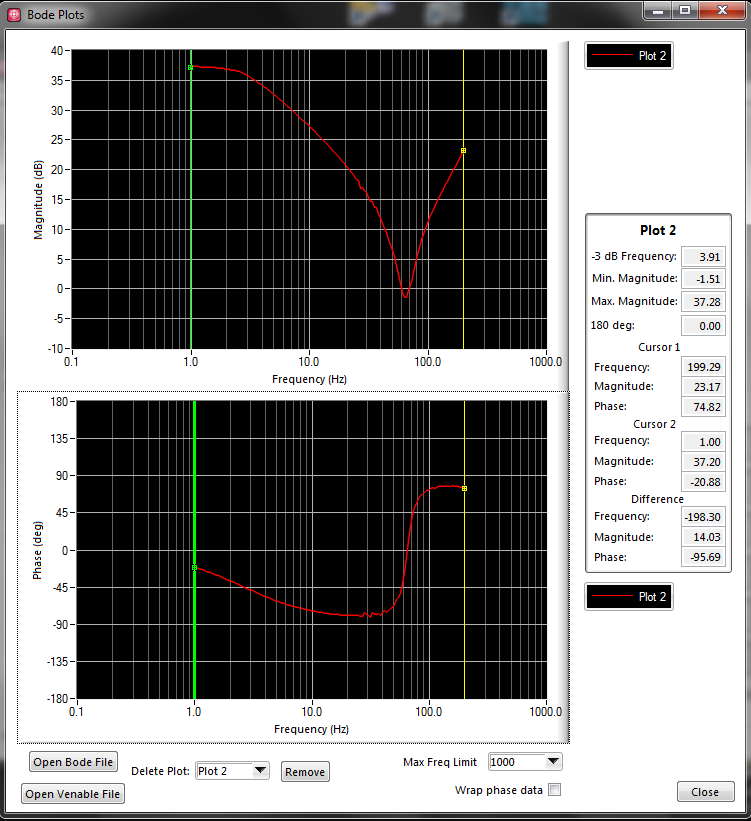
Here is a plot of the data produced:
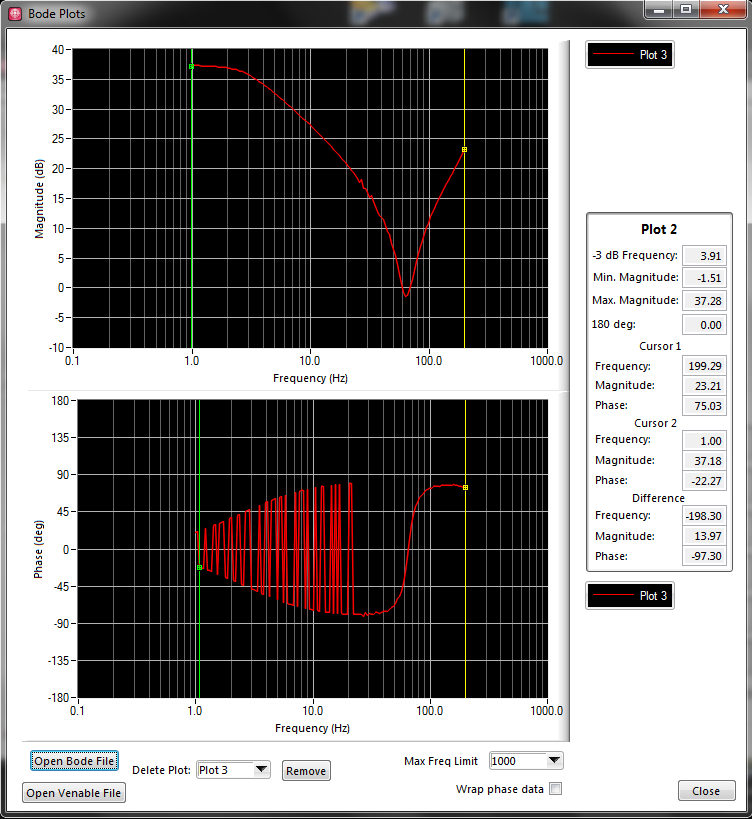
This is what is expected:
Here are both overlayed:
The expected plot was produced by cheating the log file. I went in and all I did was change the incorrect points to/from negative values. I want to eliminate this step. As you can see, if the incorrect data is mirrored on the zero-line, it would be what we expect. This "expected" data matches what my co-worker's analyzer hardware (Venable device) produces when used on our device.
We believe that the issue is not with the complex math performed, but an issue in the FFT function, or the selection of the index to use on the array of data.
Solved! Go to Solution.
05-19-2015 09:11 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi;
Have you been able to identify a pattern of when the data shows up mirrored? Or is it randomly?
05-19-2015 02:08 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi PedroMunoz,
It was semi-random.
With the help of a physicist with a PhD, the solution was discovered.
When an FFT is performed, the output is a complex frequency-domain signal. I convert this complex signal to magnitude and phase. The magnitude signal should contain a peak. The peak in the magnitude signal is located at the frequency that the sample represents. I had understood this.
However, the magntiude reading of the FFT output also contains a second peak. This second peak is for the negative frequency, and to analyze this data point the complex conjugate is required. This second peak should theoretically have the same amplitude, described as:
F(f) = F*(-f)
What I'm interested in retrieving is F(f). What was happening was because F(f) and F*(-f) are theoretically the same (therefore they should both register as the maximum value in the array), F*(-f) would sometimes be picked up as the maximum value in the array instead of F(f), perhaps due to noise. So I just needed to ensure I did not look at the negative frequencies in my array.
To ignore F*(-f), all I needed to do was only look at one half of my output of the FFT. When I change my code to:
TimeInMag = malloc(gSweepCountMax/2 * sizeof(double));
DontCareArr = malloc(gSweepCountMax/2 * sizeof(double));
for (i=0;i<gSweepCountMax/2;i++)
{
ToPolar (FFTSweepIn[i].real, FFTSweepIn[i].imaginary, &TimeInMag[i], &DontCareArr[i]);
}
MaxMin1D (TimeInMag, gSweepCountMax/2, &DontCare, &MaxMagIdx, &DontCare, &DontCareIdx);
I am ignoring the negative frequencies. By setting the "shift" parameter of CxFFTEx to FALSE, it organizes the positive frequencies in the first half, and then the negative frequencies in the second. I no longer pick up the wrong index, which would result in the flipped phase reading.
I hope this helps someone else in the future!
08-03-2017 10:19 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Thank you very much apbenedetti. It was really helpful
Waiting For the inner calling 🙂