- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
2D Interpolation
Solved!08-16-2012 03:43 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
I seem to be having some difficulty in understanding how the Interpolate 2D.vi function works
My goal is the following:
Say I have a 7 x 7 grid, which means there are 49 elements.
Now say that I know measured values at 5 points, and know their cartesion coordinates.
For example
_ _ _ _ _ _ _
_ 25 _ _ _ 25 _
_ _ _ _ _ _ _
_ _ _ 35 _ _ _
_ _ _ _ _ _ _
_ 25 _ _ _ 25 _
_ _ _ _ _ _ _
So I know the value is 25 at the point (1,1) and the value is 35 at (3,3)... etc
I tried using the Interpolate 2D function to generate all the other points, but I'm getting strange results. The dimensions of the output 2D array are larger than the input array, which should not be the case. I input a 7x7 array and the output of the Interpolate function is 13x13 which I can't seem to figure out.
The first thing that caught my attention is that when I generated an initial array, I filled all the cells with NaN because I did not want the function to use values of 0 in the interpolation. Is this correct?
Please see the attached VI as a simplified example of my problem. Any help would be appreciated!
Solved! Go to Solution.
08-16-2012 04:14 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@cory K wrote:
I tried using the Interpolate 2D function to generate all the other points, but I'm getting strange results. The dimensions of the output 2D array are larger than the input array, which should not be the case. I input a 7x7 array and the output of the Interpolate function is 13x13 which I can't seem to figure out.
The first thing that caught my attention is that when I generated an initial array, I filled all the cells with NaN because I did not want the function to use values of 0 in the interpolation. Is this correct?
Alright I seem to have this part answered. The reason the array in changing size is due to the "ntimes" input parameter. By default, this number is 1, so it will double the size of the array in each direction, in a sense quadrupling the resolution. When this number is set to 0, you get your exact array back. When you increase the number, you get a finer and finer mesh.
However, I am still stuck back at my original problem. The function is not interpolating and replacing the NaN values, it is keeping those in place.
08-17-2012 08:23 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
bump
08-17-2012 09:52 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Here is an image that hopefully conveys the idea better.
I have data that looks like this, but a bit more complicated
I would like to take those points, and interpolate between them and create something like this (from Wikipedia page on Bilinear Interpolation)
However the Interpolate function does not overwrite NaN values, so the algorithm doesn't work quite correctly.
08-17-2012 10:18 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Altenbach has some good advices on 2d interpolation...
08-17-2012 10:26 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
X = rand(5, 5);
Y = rand(5, 5);
Z = X.^2+Y.^2;
[XS, YS] = meshgrid(0:0.1:1);
[XS, YS, ZS] = griddata(X, Y, Z, XS, YS, 'v4');
surf(XS, YS, ZS)
I think the X and Y vectors (or matricies if that is easier) are relatively straight forward.
In my example, they would simply be X = [0, 1, 2, 3, 4] and Y = [0, 1, 2, 3, 4].
I think my difficulty lies in the Z matrix. I only have points sporatically, and am not sure what to put in the 'fillers' besides NaN.
In the above example, they generate a Z value at every single point using the formula "Z = X.^2+Y.^2", so they do not run into the issue of having missing points.
08-17-2012 10:57 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Eureka ![]()
It ended up being Interpolate 2D Scattered.vi that did the trick.
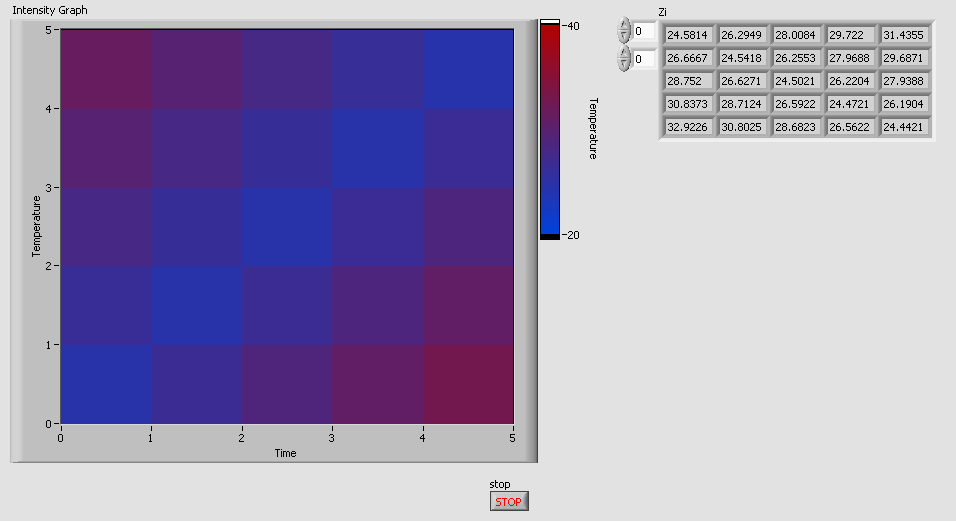
Now that all the NaN's are replaced, I get a nice complete field.
08-17-2012 10:59 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Do you have any theory about the shape of the function? Your current 5 points are not very distinct. Maybe you can fit it to a 2D polynomial surface of e.g. second order. Currently, you only have 5 points, so the number of terms is severly limited. In any case, maybe this example will help (posted here).
08-17-2012 11:05 AM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
@altenbach wrote:
Do you have any theory about the shape of the function? Your current 5 points are not very distinct. Maybe you can fit it to a 2D polynomial surface of e.g. second order. Currently, you only have 5 points, so the number of terms is severly limited. In any case, maybe this example will help (posted here).
The shape describing the function is very complicated. The example I showed was very simplified just so I could get my idea across.
In the actual application will be a large soil tank with about 90 thermocouples throughout the soil along a 2D plane. I just needed a way to display these temperatures on an intensity plot if they are not in a nice evenly spaced array.
Regarding the governing function, it is a heat flow problem, but the heat source is not a single point and is transient, so analytically describing the problem is a bit complicated. In fact, we have a PhD student working on that side of the project as we speak ![]()
05-27-2014 03:42 PM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report to a Moderator
Hi Cory_K
Could you upload .vi?