-
Analysis & Computation
297 -
Development & API
2 -
Development Tools
1 -
Execution & Performance
1,003 -
Feed management
1 -
HW Connectivity
112 -
Installation & Upgrade
264 -
Networking Communications
181 -
Package creation
1 -
Package distribution
1 -
Third party integration & APIs
278 -
UI & Usability
5,374 -
VeriStand
1
- New 2,989
- Under Consideration 1
- In Development 3
- In Beta 0
- Declined 2,625
- Duplicate 705
- Completed 324
- Already Implemented 113
- Archived 0
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
Fix (logical) inconsistency in Square function
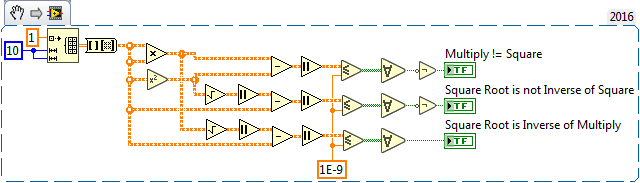
Quite by accident, I stumbled upon an inconsistency in LabVIEW's "Square" function. For almost all operations, you get the same result if you wire a numeric or "structured" numeric (like an Array or Cluster) to either Square or to both inputs of Multiply. Furthermore, you get the same (or a close approximation to the same) result if you compare the input to Square to the output from Square -> Square Root. Here's an example for a 10x10 Array of 1's -- if you run this, both Booleans will return True. Note that I'm testing for "Equality of Dbls" by subtracting them, taking their absolute value, and saying they're equal if their difference is <= 0.000000001.
However, if you transform the Square Array to a Square Matrix, Multiply still does what (mathematically) Multiply should do for a Matrix, namely do a Matrix multiplication (giving a 10x10 Matrix of 10), but Square, instead, simply squares each Matrix entry, giving a 10x10 Matrix of 1. Curiously, the Square Root function does do a proper Matrix Square Root, i.e. it produces the Matrix that, when multiplied by itself, gives the argument to the Square Root (shown by "Square Root is Inverse of Multiply").
So here we have a double-inconsistency. We have a Square function that does not always produce the same quantity as "Multiply something by itself", and a Square function that is not the inverse of the Square Root function, meaning you don't get back the same thing if you Square (a Matrix) then take its Square Root, or vice versa.
There is no "warning" (that I've seen) that Square has this anomalous behavior. It was pointed out to me (by an NI AE) that there is a listing of functions that "work" for Matrices, listing Square Root, but not Square.
At the risk of potentially causing code written with the "old" mathematically-wrong Square function to fail if migrated to a function that (mathematically) works properly for Matrices (i.e. is the inverse of Square Root and gives the same thing as "multiply by yourself"), I recommend that NI:
- Fix the Square function for Matrices so that it multiplies the matrix by itself, and
- Prominently note that the functionality of Square has been "corrected in this Version of LabVIEW", including on the Help for the Square function.
Bob Schor
P.S. -- I searched the Idea Exchange for "Matrix" and found no other mention of this "bug". It occurs to me that while NI might be reluctant to admit this is a clear bug and to fix it, potentially causing "old code moved to a new Version" to break, I strongly suspect that anyone actually using matrices in LabVIEW would already "know" that Square is broken and therefore not use it for fear of having code that "doesn't do what it seems to say it is doing", a further argument that this should really be fixed!
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.


Moved to CAR Database: CAR 629759