View Ideas...
Labels
-
Analysis & Computation
297 -
Development & API
2 -
Development Tools
1 -
Execution & Performance
1,002 -
Feed management
1 -
HW Connectivity
112 -
Installation & Upgrade
264 -
Networking Communications
181 -
Package creation
1 -
Package distribution
1 -
Third party integration & APIs
278 -
UI & Usability
5,369 -
VeriStand
1
Idea Statuses
- New 2,983
- Under Consideration 1
- In Development 3
- In Beta 0
- Declined 2,625
- Duplicate 705
- Completed 324
- Already Implemented 113
- Archived 0
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Options
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report to a Moderator
0
Kudos
Correcting round function / new correct round function
Submitted by
 MimiKLM
on
06-21-2013
05:50 PM
19 Comments (19 New)
MimiKLM
on
06-21-2013
05:50 PM
19 Comments (19 New)
Status:
Declined
Hi,
I'm bit afraid to post this idea, because it seems to be I could overlook something.
There is no function which do the proper rounding (with 5 a a last digit as a hard limit) as below:
If the last digit is 5 o greater round up, otherwise round down.
An example:
(to simplify I use only one digit after dot)
0.1 -> 0
0.4 -> 0
0.5 -> 1
0.9 -> 1
1.1 -> 1
1.4 -> 1
1.5 -> 2
1.9 -> 2
2.1 -> 2
etc.
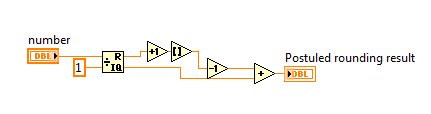
Now to satisfy this function you have to do coding like this (just for numbers with one digit after the dot):
Why to complicate so simple thing???
- Tags:
- rounding
19 Comments
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.

Any idea that has not received any kudos within a year after posting will be automatically declined.